Intervalos en Matemáticas
Un intervalo es un conjunto de números comprendidos entre dos valores, a y b, llamados extremos del intervalo, donde a < b. Los intervalos permiten describir de forma precisa un rango continuo de valores dentro de la recta real.
Intervalos Abiertos y Cerrados
Según los extremos que incluyan, los intervalos pueden clasificarse de distintas maneras:
- Intervalo cerrado [a,b]: incluye ambos extremos.
$$ [a,b] = \{ x \in R: a \le x \le b \} $$

- Intervalo abierto (a,b): excluye ambos extremos.
$$ (a,b) = \{ x \in R: a < x < b \} $$
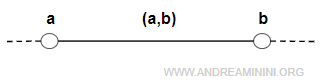
Nota. Los valores a y b siempre se consideran los extremos, tanto si el intervalo es abierto como si es cerrado.
También existen los llamados intervalos mixtos, en los que solo uno de los extremos forma parte del conjunto:
- Abierto por la izquierda y cerrado por la derecha (a,b], lo que indica que b pertenece al intervalo, pero a no:
$$ (a,b] = \{ x \in R: a < x \le b \} $$
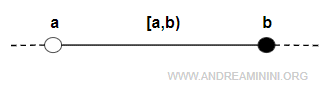
- Cerrado por la izquierda y abierto por la derecha [a,b), donde a está incluido pero b no:
$$ [a,b) = \{ x \in R: a \le x < b \} $$
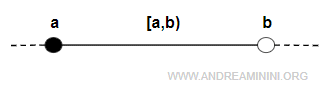
Intervalos Acotados y No Acotados
Otra forma de clasificar los intervalos depende de si sus límites son finitos o no:
- Intervalo acotado: ambos extremos son números reales finitos.
$$ (a,b) $$ - Intervalo no acotado: al menos uno de los extremos es ±∞.
$$ (a,+\infty) \\ (-\infty, b) \\ (-\infty,+\infty) = R $$
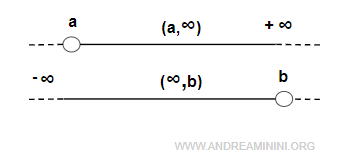
Nota. En los intervalos no acotados, el infinito siempre se considera un extremo abierto, ya que no representa un número real sino una idea: la de una extensión ilimitada. Un intervalo puede carecer de límite superior, de límite inferior o de ambos, como en (a,+∞) o (-∞,b). El extremo finito, en cambio, puede ser cerrado, como en [a,+∞) o (-∞,b], o abierto, como en (a,+∞) o (-∞,b).
Los intervalos son fundamentales en matemáticas porque permiten describir con claridad conjuntos continuos de valores, un concepto esencial en el análisis, la geometría y muchas aplicaciones científicas.