Propiedades de las Operaciones Matemáticas
Las propiedades formales de las operaciones matemáticas incluyen las siguientes:
Propiedad Conmutativa
Propiedad Conmutativa de la Suma
En la suma, el orden de los sumandos no altera el resultado. $$ a + b = b + a $$
Por ejemplo:
$$ 4 + 3 = 3 + 4 $$
$$ 7 = 7 $$
No obstante, la propiedad conmutativa no se cumple en la resta.
Por ejemplo:
$$ 4 - 3 \ne 3 - 4 $$
$$ 1 \ne -1 $$
Propiedad Conmutativa de la Multiplicación
En la multiplicación, el orden de los factores no modifica el producto.
Por ejemplo:
$$ 4 \cdot 3 = 3 \cdot 4 $$
$$ 12 = 12 $$
En cambio, la propiedad conmutativa no se cumple en la división.
Por ejemplo:
$$ 10 : 5 \ne 5 : 10 $$
$$ 2 \ne 0,5 $$
Propiedad Asociativa
Propiedad Asociativa de la Suma
La suma de tres números, a, b y c, no varía aunque se agrupen de diferente manera, siempre que se conserve el orden de los sumandos. $$ (a + b) + c = a + (b + c) $$
Por ejemplo:
$$ (2 + 5) + 3 = 2 + (5 + 3) $$
$$ 7 + 3 = 2 + 8 $$
$$ 10 = 10 $$
Sin embargo, la propiedad asociativa no se cumple en la resta.
Por ejemplo:
$$ (2 - 5) - 3 \ne 2 - (5 - 3) $$
$$ -3 - 3 \ne 2 - 2 $$
$$ -6 \ne 0 $$
Propiedad Asociativa de la Multiplicación
El producto de tres números, a, b y c, permanece igual sin importar cómo se agrupen los factores, siempre que su orden no cambie. $$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
Por ejemplo:
$$ (2 \cdot 5) \cdot 3 = 2 \cdot (5 \cdot 3) $$
$$ 10 \cdot 3 = 2 \cdot 15 $$
$$ 30 = 30 $$
En cambio, la propiedad asociativa no se cumple en la división.
$$ (8 : 4) : 2 \ne 8 : (4 : 2) $$
$$ 2 : 2 \ne 8 : 2 $$
$$ 1 \ne 4 $$
Propiedad Distributiva
Propiedad Distributiva de la Multiplicación respecto de la Suma
Multiplicar un número a por la suma (b + c) es equivalente a multiplicar a por cada sumando y luego sumar los resultados. $$ a \cdot (b + c) = a \cdot b + a \cdot c $$
Por ejemplo:
$$ 2 \cdot (3 + 4) = 2 \cdot 3 + 2 \cdot 4 $$
$$ 2 \cdot 7 = 6 + 8 $$
$$ 14 = 14 $$
La propiedad distributiva de la multiplicación respecto de la suma se cumple tanto si se multiplica a la izquierda como a la derecha, ya que la multiplicación es conmutativa.
$$ (3 + 4) \cdot 2 = 3 \cdot 2 + 4 \cdot 2 $$
$$ 7 \cdot 2 = 6 + 8 $$
$$ 14 = 14 $$
La propiedad distributiva también se aplica a la resta:
$$ (4 - 3) \cdot 2 = 4 \cdot 2 - 3 \cdot 2 $$
$$ 1 \cdot 2 = 8 - 6 $$
$$ 2 = 2 $$
Demostración Geométrica
La propiedad distributiva de la multiplicación sobre la suma puede demostrarse geométricamente.
Consideremos un rectángulo con base \( a \) y altura \( (b + c) \).
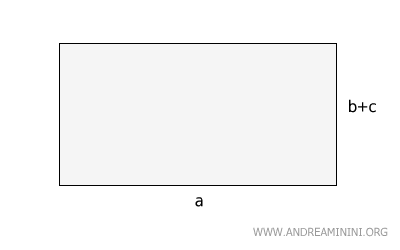
El área $ A $ del rectángulo se obtiene multiplicando la base por la altura:
$$ A = a \cdot (b + c) $$
Si dividimos la altura en dos segmentos, \( b \) y \( c \), obtenemos dos rectángulos más pequeños, ambos con la misma base \( a \), pero con alturas \( b \) y \( c \), respectivamente.
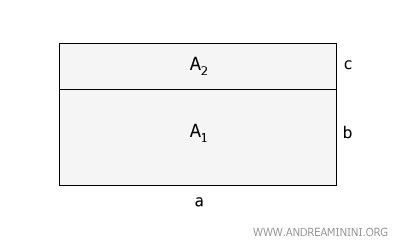
La suma de las áreas de estos dos rectángulos, $ A_1 + A_2 $, coincide con el área total $ A $.
$$ A = A_1 + A_2 $$
Como $ A = a \cdot (b + c) $, y $ A_1 = a \cdot b $ mientras que $ A_2 = a \cdot c $, se concluye que:
$$ a \cdot (b + c) = a \cdot b + a \cdot c $$
Así, queda demostrada la propiedad distributiva de la multiplicación respecto de la suma mediante una descomposición geométrica utilizando números naturales.
En otras palabras, el área total del rectángulo puede considerarse como un solo rectángulo de altura \( b + c \), o como la suma de las áreas de dos rectángulos más pequeños.
Nota: La propiedad distributiva no es aplicable en sentido inverso, es decir, no se puede “distribuir” la suma sobre la multiplicación. $$ 2 + (3 \cdot 4) \ne (2 + 3) \cdot (2 + 4) $$ $$ 2 + 12 \ne 5 \cdot 6 $$ $$ 14 \ne 30 $$
Propiedad Distributiva de la División respecto de la Suma
Dividir una suma (a + b) entre un número c distinto de cero equivale a dividir cada término por c y luego sumar los resultados. $$ (a + b) : c = a : c + b : c $$
Por ejemplo:
$$ (4 + 8) : 2 = 4 : 2 + 8 : 2 $$
$$ 12 : 2 = 2 + 4 $$
$$ 6 = 6 $$
Nota: La propiedad distributiva de la división se aplica tanto a la suma como a la resta. $$ (4 - 8) : 2 = 4 : 2 - 8 : 2 $$ $$ -4 : 2 = 2 - 4 $$ $$ -2 = -2 $$
No obstante, la propiedad distributiva de la división sobre la suma solo es válida cuando la división se realiza desde la izquierda, ya que la división no es una operación conmutativa.
$$ 10 : (2 + 5) \ne 10 : 2 + 10 : 5 $$
$$ 10 : 7 \ne 5 + 2 $$
$$ 10 : 7 \ne 7 $$
Y así sucesivamente.