Conjuntos numéricos

En matemáticas, los números no se consideran de forma aislada, sino que se organizan en conjuntos. Cada conjunto responde a una necesidad concreta y amplía progresivamente el tipo de cantidades que podemos describir y calcular. A continuación se presentan los principales conjuntos numéricos.

• Conjunto de los números naturales (N)
  Este conjunto reúne los enteros positivos que se utilizan para contar objetos y medir cantidades discretas. Es el sistema numérico más antiguo y el más intuitivo, ya que surge directamente de la experiencia cotidiana.

  Conjunto de los números naturales con cero N₀
  Esta ampliación de los números naturales incluye también el cero, lo que permite representar de manera explícita la ausencia de elementos o una cantidad nula.

• Conjunto de los números enteros (Z)
  El conjunto de los números enteros extiende a los naturales al incorporar los valores negativos y el cero. Gracias a ello es posible describir situaciones como ganancias y pérdidas, desplazamientos con sentido opuesto o diferencias entre cantidades. Los números naturales forman un subconjunto de este conjunto.
• Conjunto de los números racionales (Q)
  Los números racionales son aquellos que pueden escribirse como el cociente de dos números enteros con denominador distinto de cero. Incluyen tanto las fracciones como los números decimales con desarrollo finito o periódico. Todos los números enteros pertenecen también a este conjunto.
• Conjunto de los números irracionales (I)
  Este conjunto está formado por números reales que no pueden expresarse como el cociente de dos enteros. Sus desarrollos decimales son infinitos y no periódicos. Los números irracionales no pertenecen al conjunto de los racionales.
• Conjunto de los números reales (R)
  Los números reales se obtienen como la unión de los números racionales y los irracionales. En conjunto forman un continuo que puede identificarse con todos los puntos de la recta real y que permite representar cualquier magnitud real.
  
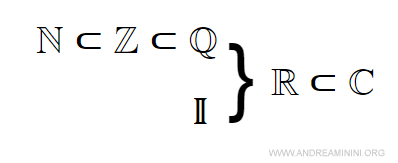
• Conjunto de los números complejos (C)
  El conjunto de los números complejos amplía el de los números reales al incluir soluciones de ecuaciones que implican raíces cuadradas de números negativos. Cada número complejo puede representarse en la forma a + bi, donde a y b son números reales e i es la unidad imaginaria.