Principio de Conservación de la Energía
El principio de conservación de la energía afirma que, en un sistema aislado, la cantidad total de energía permanece inalterada a lo largo del tiempo.
En pocas palabras, la energía no puede crearse ni destruirse: únicamente puede transformarse de una forma en otra. Este principio constituye uno de los pilares fundamentales de la física.
Se cumple sin importar la modalidad de energía (cinética, potencial, térmica, química, etc.) y mantiene su validez en cada transformación de un tipo de energía en otro.
- Energía cinética ($E_k$): asociada al movimiento
- Energía potencial ($E_p$): asociada a la posición en un campo de fuerzas
- Energía térmica: vinculada al movimiento de las partículas
- Energía química, eléctrica, nuclear, radiante, entre otras...
Existe, no obstante, una condición esencial: el sistema debe ser un sistema aislado, es decir, que no intercambie energía (ni materia) con el entorno.
Si esta condición no se cumple, el balance energético queda abierto: la energía puede entrar o salir del sistema.
Ley de Conservación de la Energía
En un sistema mecánico simple (sin rozamiento), la energía total se mantiene constante y puede expresarse como:
$$ E = E_p + E_k = \text{constante} $$
donde $E_p$ representa la energía potencial y $E_k$ la energía cinética.
En un caso más general, cuando intervienen varias formas de energía:
$$ E_{\text{total}} = E_{\text{cinética}} + E_{\text{potencial}} + E_{\text{térmica}} + \dots = \text{constante} $$
La energía total solo se conserva si se contabilizan todas las formas presentes y no hay intercambio con el exterior; en otras palabras, cuando el sistema es realmente aislado.
Ejemplos
Ejemplo 1 - Caída libre
Imaginemos dejar caer una esfera desde una altura $h$, sin resistencia del aire.
Al inicio, mientras la esfera permanece en la mano, toda la energía es potencial: $E_p = mgh$, sin contribución cinética.
Al soltarla, la energía potencial disminuye a medida que desciende, mientras la energía cinética aumenta.
La energía no desaparece: simplemente se transforma de un tipo en otro.
$$ E_k(t) + E_p(t) = \text{constante} $$
Poco antes de tocar el suelo, la energía potencial es prácticamente nula ($E_p \approx 0$) y la energía cinética alcanza su valor máximo: $E_k = \tfrac{1}{2}mv^2$.
Ejemplo resuelto. Consideremos una esfera de masa $m = 0.5 \,\text{kg}$ que cae desde una altura $h = 2 \,\text{m}$, despreciando la resistencia del aire. Inicialmente, toda la energía es potencial: $$ E_p = m g h = 0.5 \cdot 9.81 \cdot 2 \approx 9.81 \,\text{J} $$ mientras que la energía cinética es nula: $$E_k = 0 $$ Así, la energía total inicial del sistema es: $$E_{\text{tot}} = 9.81 \,\text{J}$$ A la mitad de la altura $(h/2 = 1 \,\text{m})$, la energía se reparte en partes iguales: la mitad sigue siendo potencial y la otra mitad ya se ha convertido en cinética. $$ E_p = m g h/2 = 0.5 \cdot 9.81 \cdot 1 = 4.905 \,\text{J} $$ $$ E_k = E_{\text{tot}} - E_p = 9.81 - 4.905 = 4.905 \,\text{J} $$ La energía total permanece invariable: $$ E_{\text{tot}} = E_p + E_k = 4.905 \,\text{J} + 4.905 \,\text{J} = 9.81 \,\text{J} $$ La velocidad en este punto intermedio es: $$ E_k = \tfrac{1}{2} m v^2 \;\;\Rightarrow\;\; v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 4.905}{0.5}} \approx 4.43 \,\text{m/s} $$ Justo antes del impacto, la energía potencial es prácticamente nula: $$ E_p \approx 0 $$ mientras la cinética alcanza su valor máximo: $$ E_k = E_{\text{tot}} = 9.81 \,\text{J} $$ La velocidad de impacto será: $$ v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 9.81}{0.5}} = \sqrt{39.24} \approx 6.26 \,\text{m/s} $$ En conclusión, durante toda la caída, la suma de energía potencial y cinética permanece constante: $$ E_{\text{total}} = E_p + E_k = 9.81 \,\text{J} = \text{constante} $$ Ninguna energía se pierde: únicamente se transforma de potencial gravitatoria en cinética.
Ejemplo 2 - Péndulo oscilante
En un péndulo ideal (sin fricción), la energía potencial alcanza su máximo en los extremos, cuando la velocidad es nula y el péndulo se detiene antes de invertir el movimiento.
En la posición más baja, la energía cinética es máxima, ya que el péndulo alcanza su mayor velocidad.
Una vez más:
$$ E_k + E_p = \text{constante} $$
Nota. Si se tiene en cuenta la resistencia del aire, la energía mecánica se iría transformando gradualmente en calor en lugar de conservarse por completo. Sin embargo, la suma global (mecánica + térmica) seguiría siendo constante. El principio de conservación de la energía permanece válido.
Ejemplo 3 - Conversión de energía en una central eléctrica
En una central termoeléctrica, la energía química del combustible se libera mediante combustión.
La combustión genera gases calientes que transfieren energía térmica a un fluido de trabajo (normalmente agua), convirtiéndolo en vapor a alta presión.
Ese vapor acciona una turbina, transformando la energía térmica en energía mecánica de rotación.
La turbina está conectada a un generador, que convierte la energía mecánica en energía eléctrica mediante inducción electromagnética.
En cada etapa, la energía total se conserva: únicamente cambia de forma.
Nota. No toda la energía térmica se transforma; una parte se pierde inevitablemente en forma de calor residual. Aun así, en un sistema aislado, la suma de la electricidad útil generada y el calor disipado permanece constante. El principio de conservación nunca se ve vulnerado.
Conservación de la Energía en la Física de Partículas
El principio de conservación de la energía es auténticamente universal: se cumple en todas las interacciones fundamentales. Ya sea en desintegraciones, colisiones o aniquilaciones, la energía total antes y después del proceso permanece inalterada.
Un buen ejemplo es la desintegración beta. En este fenómeno, un neutrón se transforma en un protón, un electrón y un antineutrino $ n \;\;\longrightarrow\;\; p + e^- + \bar{\nu}_e $, a través de la interacción nuclear débil.
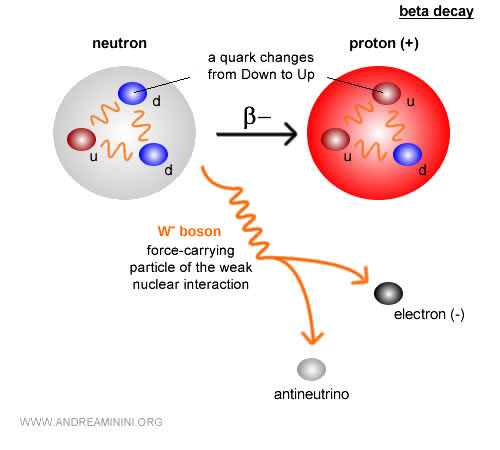
Aquí, la masa en reposo no se conserva: la masa del neutrón es mayor que la suma de las masas del protón, el electrón y el antineutrino.
Esa masa “faltante” no desaparece: se transforma en energía cinética de las partículas emitidas.
El punto clave es que lo que permanece constante es la energía total, no la masa. Así lo expresa la célebre ecuación de Einstein:
$$ E = mc^2 $$
En otras palabras, una fracción de la masa en reposo puede convertirse en energía cinética o en radiación.
También puede ocurrir lo contrario: la energía puede transformarse en masa, por ejemplo mediante la creación de un par quark-antiquark.
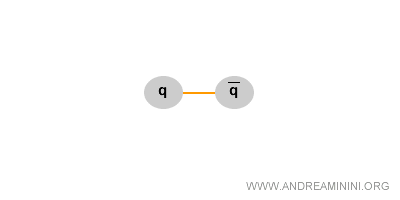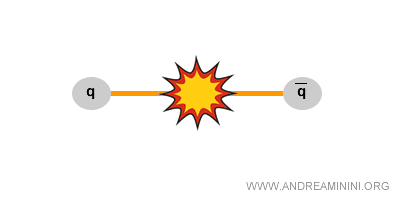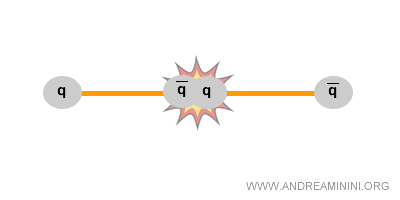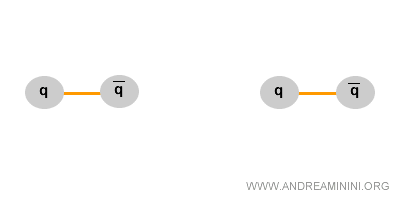
De ahí que, en las reacciones nucleares y en las desintegraciones de partículas, la masa pueda parecer “desaparecer” o “surgir”, mientras que el balance energético global permanece intacto.
Nota. Junto con la energía, en las interacciones fundamentales también se conservan otras magnitudes: el momento lineal, la carga eléctrica, la carga de color en QCD, los números leptónico y bariónico (en condiciones específicas), el espín total, entre otras.
Conservación de la Energía en el Universo
El principio de conservación de la energía se cumple con total fiabilidad en todos los contextos físicos locales, desde la mecánica cuántica no relativista hasta la teoría cuántica de campos (QFT).
No obstante, en la relatividad general la situación es más sutil. En un espacio-tiempo curvo no siempre puede definirse de manera unívoca y rigurosa una “energía total” para el universo entero.
La razón está en el teorema de Noether, que vincula la conservación de la energía con la simetría frente a traslaciones temporales. En un universo en expansión, esa simetría global del tiempo deja de existir.
Un ejemplo clásico es la expansión cósmica: la densidad de energía de la radiación disminuye más deprisa que la de la materia porque es el propio espacio el que se estira. No se trata de un “trasvase” de energía entre sectores, sino de una consecuencia geométrica de la expansión del espacio-tiempo.
Por eso muchos cosmólogos sostienen que hablar de “conservación de la energía total del universo” resulta, como mínimo, equívoco. Lo que sí se conserva es la energía a nivel local: dentro de cada proceso físico descrito en un sistema de referencia concreto.
A escala global, la cuestión sigue abierta y está íntimamente ligada al problema aún no resuelto de cómo definir de manera coherente la energía en el marco de la relatividad general.
Fundamentos Teóricos
La conservación de la energía se deriva directamente de la invariancia de las leyes físicas frente a traslaciones temporales: las leyes no cambian si un experimento se lleva a cabo hoy, mañana o dentro de siglos.
No es, por tanto, una simple regla empírica basada en observaciones.
Surge de una simetría fundamental de la naturaleza.
En física, “simetría” no significa lo mismo que en la geometría cotidiana, sino una transformación que deja inalterado el comportamiento de un sistema físico.
Por ejemplo, si un sistema se comporta de la misma manera hoy, mañana o dentro de cien años, las leyes que lo gobiernan son independientes del tiempo: son invariantes bajo traslaciones temporales.
Esta invariancia temporal garantiza que la energía total de un sistema permanezca constante a medida que transcurre el tiempo.
El vínculo profundo entre simetrías y magnitudes conservadas fue formalizado en 1918 por Emmy Noether. Según el teorema de Noether:
A toda simetría continua de un sistema físico corresponde una magnitud conservada.
En el caso de la conservación de la energía, la simetría pertinente es la invariancia bajo traslaciones temporales: si las leyes de la física no cambian con el tiempo, entonces la energía se conserva.
Este principio se cumple en todo el espectro de la física, desde la mecánica clásica hasta los marcos más avanzados de la teoría cuántica.
Y así sucesivamente.