Ensembles numériques

En mathématiques, les nombres ne sont pas étudiés isolément, mais organisés en ensembles cohérents. Chaque ensemble répond à un besoin précis et permet d'élargir progressivement le type de quantités que l'on peut décrire, comparer et calculer. Cette organisation facilite la compréhension des propriétés des nombres et de leurs relations. On présente ci-dessous les principaux ensembles numériques, tels qu'ils sont couramment utilisés en mathématiques.

• Ensemble des nombres naturels (N)
  Cet ensemble regroupe les entiers positifs employés pour compter des objets et dénombrer des quantités discrètes. Il s'agit du système numérique le plus ancien et le plus intuitif, directement issu de l'expérience du comptage.

  Ensemble des nombres naturels avec zéro N₀
  Cette extension de l'ensemble des nombres naturels inclut le zéro, ce qui permet de représenter explicitement l'absence d'éléments ou une quantité nulle.

• Ensemble des nombres entiers (Z)
  L'ensemble des nombres entiers prolonge celui des nombres naturels en y ajoutant le zéro et les entiers négatifs. Il permet de décrire des situations concrètes comme les gains et les pertes, les déplacements orientés ou les écarts entre deux quantités. Les nombres naturels forment un sous-ensemble de cet ensemble.
• Ensemble des nombres rationnels (Q)
  Les nombres rationnels sont les nombres qui peuvent s'écrire comme le quotient de deux entiers, avec un dénominateur non nul. Ils incluent les fractions ainsi que les nombres décimaux à écriture finie ou à écriture décimale infinie périodique. Tous les nombres entiers appartiennent également à cet ensemble.
• Ensemble des nombres irrationnels (I)
  Cet ensemble regroupe des nombres réels qui ne peuvent pas être exprimés comme le quotient de deux entiers. Leur écriture décimale est infinie et non périodique. Les nombres irrationnels se distinguent ainsi clairement des nombres rationnels.
• Ensemble des nombres réels (R)
  L'ensemble des nombres réels est obtenu en réunissant les nombres rationnels et les nombres irrationnels. Il forme un continuum que l'on peut représenter par la droite réelle, sur laquelle chaque point correspond à un nombre réel. Cet ensemble permet de modéliser toutes les grandeurs mesurables en mathématiques classiques.
  
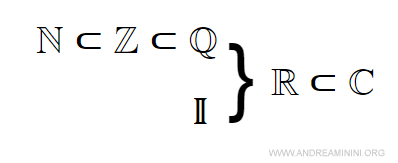
• Ensemble des nombres complexes (C)
  L'ensemble des nombres complexes élargit celui des nombres réels en introduisant des solutions à certaines équations algébriques qui n'admettent pas de solution réelle, notamment celles faisant intervenir la racine carrée de nombres négatifs. Tout nombre complexe s'écrit sous la forme a + bi, où a et b sont des nombres réels et i est l'unité imaginaire, définie par la relation i² = -1.