Gradient

Le gradient d’une fonction ou d’un champ scalaire f(x, y, z) est un champ vectoriel dont les composantes sont les dérivées partielles de f par rapport aux coordonnées cartésiennes (x, y, z). $$ \nabla f = \frac{ \partial f}{\partial x} \vec{u}_x + \frac{ \partial f}{\partial y} \vec{u}_y + \frac{ \partial f}{\partial z} \vec{u}_z $$ Cet opérateur différentiel, représenté par le symbole nabla ∇ (un triangle inversé), est aussi couramment noté grad : $$ \text{grad} \, f = \frac{ \partial f}{ \partial x} \vec{u}_x + \frac{ \partial f}{ \partial y} \vec{u}_y + \frac{ \partial f}{ \partial z} \vec{u}_z $$

Ici, u_x, u_y et u_z désignent les vecteurs unitaires orientés selon les axes x, y et z de l’espace tridimensionnel.

Le champ scalaire f(x, y, z) est une fonction à valeurs réelles, tandis que son gradient ∇f est un champ vectoriel.

Que traduit le gradient ?

Le gradient associe à un champ scalaire un champ vectoriel. Il indique à la fois la direction et l’intensité de la variation la plus forte de la grandeur considérée.

Par exemple, le gradient de température montre non seulement de quelle façon, mais surtout dans quelle direction la température varie le plus rapidement dans l’espace.

Remarque. Le gradient pointe dans la direction où le champ scalaire f(x, y, z) croît le plus rapidement. Sa norme mesure la vitesse maximale de variation en ce point.

Propriétés essentielles du gradient

Étant donné un gradient ∇f et un vecteur v, le produit scalaire ∇f · v donne la dérivée directionnelle de f dans la direction de v :

$$ \nabla f \cdot \vec{v} = D_v f $$

Qu’appelle-t-on dérivée directionnelle ? Elle mesure comment varie une fonction f(x, y, z) lorsqu’on se déplace selon une direction donnée, définie par le vecteur v : $$ D_v f = \lim_{h \to 0} \frac{f(x+h \cdot \vec{v}, \ y+h \cdot \vec{v}, \ z+h \cdot \vec{v}) - f(x, y, z)}{h} $$ Elle généralise la notion de dérivée partielle, qui ne renseigne que sur la variation le long des axes de coordonnées : $$ D_x f = \lim_{\Delta x \to 0} \frac{f(x+\Delta x, y, z) - f(x, y, z)}{\Delta x} $$

Si l’on considère un déplacement infinitésimal dans la direction du vecteur de position v (vecteur de position) :

$$ d \vec{v} = dx \cdot \vec{u}_x + dy \cdot \vec{u}_y + dz \cdot \vec{u}_z $$

La dérivée directionnelle de f dans cette direction s’exprime à l’aide du gradient :

$$ \frac{d \ f(\vec{v})}{d \ \vec{v}} = \nabla f $$

Le différentiel de la fonction dans la direction de v est donc :

$$ df(\vec{v}) = \nabla f \cdot d \vec{v} $$

D’où l’approximation de la valeur de la fonction en un point voisin :

$$ f(\vec{v} + d \vec{v}) = f(\vec{v}) + df(\vec{v}) = f(\vec{v}) + \nabla f(\vec{v}) \cdot \vec{v} $$

Un exemple concret

Considérons une fonction de deux variables :

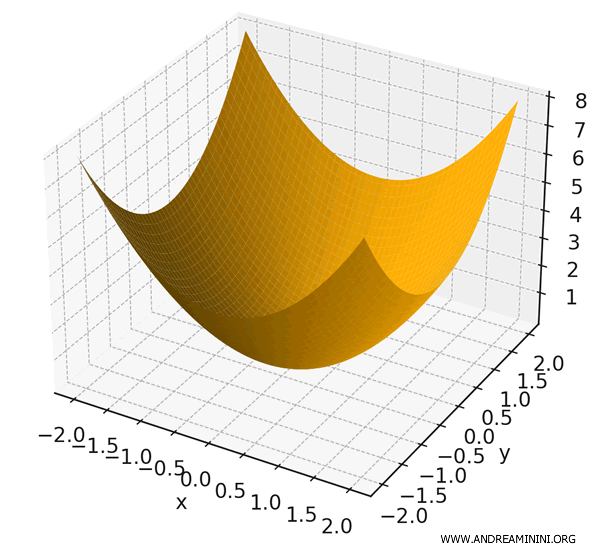
\[ f(x, y) = x^2 + y^2 \]

Cette fonction associe à chaque point \( (x, y) \) le carré de sa distance à l’origine.

Pour calculer le gradient \( \nabla f \), dérivons partiellement par rapport à \( x \) et \( y \) :

\[ \frac{\partial f}{\partial x} = 2x \]

\[ \frac{\partial f}{\partial y} = 2y \]

On obtient ainsi :

\[ \nabla f(x, y) = 2x \, \vec{u}_x + 2y \, \vec{u}_y \]

En écriture vectorielle :

\[ \nabla f(x, y) = \begin{pmatrix} 2x \\ 2y \end{pmatrix} \]

Les vecteurs du gradient pointent radialement vers l’extérieur à partir de l’origine. Cela traduit le fait que la fonction \( f(x, y) = x^2 + y^2 \) croît le plus rapidement dans la direction radiale.

La norme du gradient est \( |\nabla f| = \sqrt{(2x)^2 + (2y)^2} = 2\sqrt{x^2 + y^2} \), ce qui indique la vitesse à laquelle la fonction augmente à mesure que l’on s’éloigne de l’origine.

Par exemple, au point \( (1, 2) \) :

\[ \nabla f(1, 2) = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} \]

Cela signifie qu’en \( (1, 2) \), la fonction croît le plus vite dans la direction du vecteur \( (2, 4) \), qui pointe vers le point \( (3, 6) \).

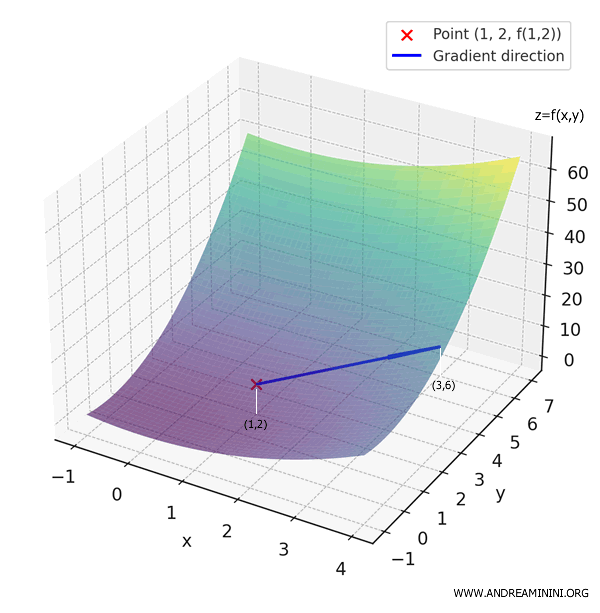
On peut répéter ce raisonnement en tout point du plan \( (x, y) \).

On obtient ainsi le champ vectoriel du gradient de la fonction \( f(x, y) = x^2 + y^2 \) :

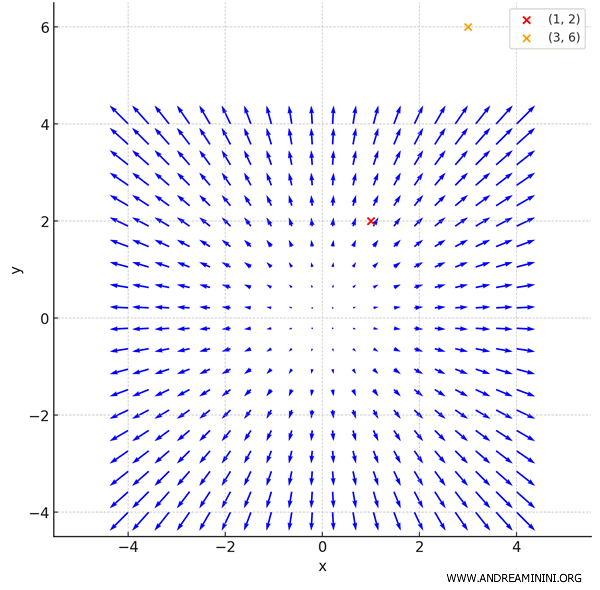
Chaque flèche représente le vecteur gradient en un point donné \( (x, y) \).

Tous les vecteurs sont orientés vers l’extérieur, puisque la fonction augmente avec la distance à l’origine.

Les points \( (1, 2) \) et \( (3, 6) \) sont indiqués respectivement en rouge et en orange.

On peut également ajouter des courbes de niveau, qui correspondent aux lieux géométriques où la fonction prend une valeur constante \( f(x, y) = c \).

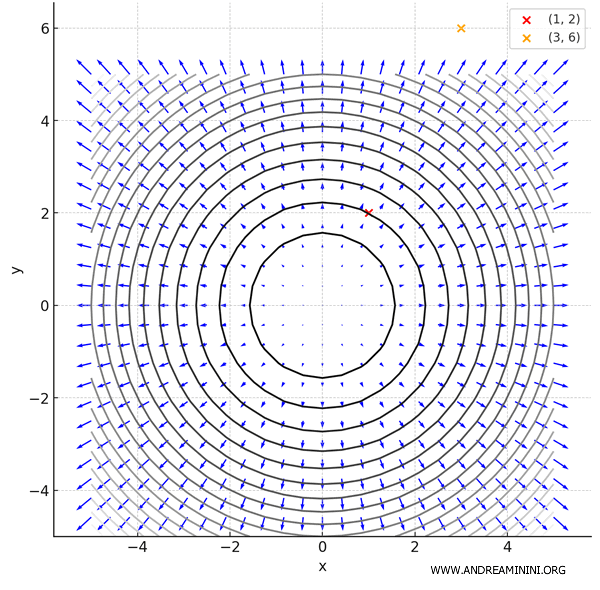
Dans ce cas, les courbes de niveau sont des cercles concentriques, puisque \( f(x, y) = x^2 + y^2 \).

Le gradient indique la direction de variation maximale

Le gradient \( \nabla f(x_0) \) est un vecteur qui désigne la direction dans laquelle la fonction croît le plus rapidement.

Autrement dit, il pointe vers la pente la plus raide, c’est-à-dire l’orientation suivant laquelle la fonction connaît le taux d’accroissement le plus élevé.

La norme du gradient mesure précisément ce taux de variation dans cette direction.

À l’inverse, la direction de décroissance la plus rapide correspond au vecteur gradient pris avec un signe négatif.

Exemple

Considérons la fonction suivante :

$$ f(x,y) = x^2 + y^2 $$

C’est l’équation d’une surface en forme de paraboloïde circulaire, un cas classique déjà rencontré.

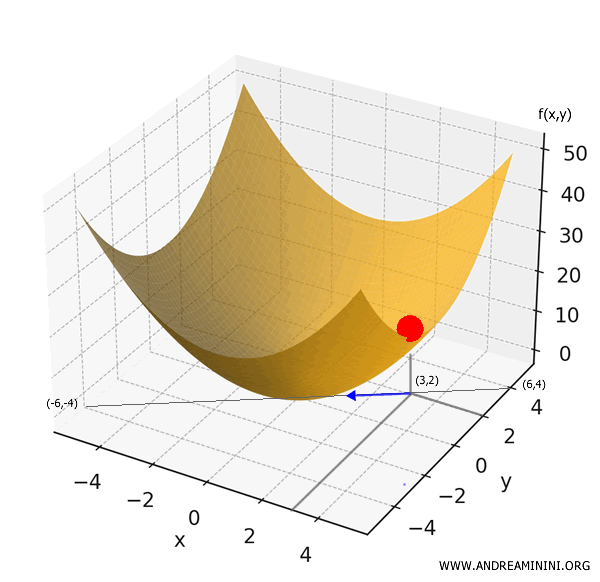
Supposons que l’on laisse tomber une bille au point (3,2). Dans quelle direction commencera-t-elle à rouler ?

Pour répondre, calculons d’abord les dérivées partielles de la fonction par rapport à \( x \) et \( y \) :

$$ f_x = 2x $$

$$ f_y = 2y $$

On peut alors construire le vecteur gradient de la fonction :

$$ \nabla f(x,y) = (2x, 2y) $$

En évaluant le gradient au point (3,2), on obtient :

$$ \nabla f(3,2) = (2 \cdot 3, 2 \cdot 2) = (6, 4) $$

Le vecteur gradient pointe toujours dans la direction de la croissance maximale de la fonction, c’est-à-dire là où elle augmente le plus rapidement.

Cependant, la bille étant soumise à la gravité, elle descendra la pente : elle roulera donc dans la direction de la décroissance la plus forte, c’est-à-dire l’opposée du gradient :

$$ -\nabla f(3,2) = (-6, -4) $$

La bille se déplacera ainsi dans la direction du vecteur \( (-6, -4) \).

Remarque. On peut aussi normaliser ce vecteur directionnel afin d’obtenir un vecteur unitaire pointant dans la même direction : \[ \mathbf{u} = \frac{-\nabla f(3,2)}{\lVert \nabla f(3,2) \rVert} = \frac{(-6, -4)}{\sqrt{6^2 + 4^2}} = \Bigl(-\tfrac{3}{\sqrt{13}},\, -\tfrac{2}{\sqrt{13}}\Bigr) \] La normalisation permet de décrire uniquement la direction, indépendamment de la pente ou de la vitesse. L’interprétation géométrique et physique demeure inchangée.

Démonstration

Pour justifier ce résultat, partons de la définition de la dérivée directionnelle d’une fonction \( f \) en un point \( x_0 \), dans la direction d’un vecteur \( \vec{v} \).

La dérivée directionnelle s’exprime comme le produit scalaire du gradient de \( f \) en \( x_0 \) avec le vecteur directionnel \( \vec{v} \) :

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \nabla f(x_0) \cdot \vec{v} \]

À l’aide de la définition géométrique du produit scalaire, on obtient :

\[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \]

Ici, \( \theta \) désigne l’angle formé par le gradient \( \nabla f(x_0) \) et le vecteur directionnel \( \vec{v} \).

Cette relation montre que la dérivée directionnelle dépend de trois facteurs :

1. La norme du gradient, qui exprime la rapidité de variation de la fonction en ce point ;
2. La norme du vecteur directionnel \( \vec{v} \), généralement choisi unitaire ( \( |\vec{v}| = 1 \) ) ;
3. Le cosinus de l’angle \( \theta \) entre le gradient et la direction choisie.

Comme la norme du gradient est indépendante de la direction, et que l’on travaille le plus souvent avec des vecteurs unitaires, la valeur de la dérivée directionnelle dépend essentiellement de \( \cos\theta \).

Examinons quelques cas particuliers :

• Si \( \theta = 0^\circ \), alors \( \cos\theta = 1 \) : les vecteurs sont colinéaires et de même sens. La dérivée directionnelle atteint sa valeur maximale, dans la direction du gradient.
• Si \( \theta = 180^\circ \), alors \( \cos\theta = -1 \) : les vecteurs sont colinéaires mais de sens opposé. La dérivée directionnelle prend sa valeur minimale, dans la direction opposée au gradient.
• Si \( \theta = 90^\circ \), alors \( \cos\theta = 0 \) : les vecteurs sont orthogonaux. La dérivée directionnelle est nulle, la fonction ne varie donc pas dans cette direction.

On en conclut que le gradient \( \nabla f(x_0) \) indique non seulement la direction de la variation maximale, mais que sa norme représente également le taux maximal de variation de la fonction en ce point.

Relation entre gradient et courbes de niveau

Le gradient est toujours perpendiculaire aux courbes de niveau.

Autrement dit, si l’on trace une courbe de niveau - par exemple un cercle -, le gradient en tout point de cette courbe est un vecteur orthogonal, orienté radialement vers l’extérieur.

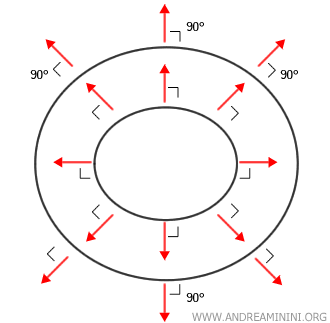
Les courbes de niveau représentent l’ensemble des points où la fonction garde une valeur constante, soit $ f(x,y) = c $.

Le gradient, lui, indique la direction de la croissance maximale : $ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) $.

Ainsi, si la fonction reste constante le long d’une courbe de niveau et croît dans une direction différente, ces deux directions sont nécessairement perpendiculaires.

Exemple

Le gradient de la fonction $ f(x,y) = x^2 + y^2 $ définit un champ vectoriel qui associe à chaque point du plan un vecteur indiquant la direction de croissance maximale, et par symétrie, celle de décroissance la plus forte.

On observe que le vecteur gradient en tout point $ (x,y,z) $ de la surface $ z = f(x,y) $ est perpendiculaire à la courbe de niveau passant par ce point.

Le seul point où le gradient s’annule est l’origine, $ (x,y,z) = (0,0,0) $, centre des courbes de niveau de cette fonction : à cet endroit, le vecteur est nul et n’a pas de direction.

Remarque. Un gradient nul correspond à un point critique, c’est-à-dire un point où la fonction ne varie dans aucune direction. Pour analyser la nature de ce point, on calcule le laplacien, défini comme la somme des dérivées partielles secondes : \[\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\] La valeur du laplacien permet alors de caractériser le point critique : si \( \Delta f > 0 \), il s’agit d’un minimum local ; si \( \Delta f < 0 \), d’un maximum local ; et si \( \Delta f = 0 \), le test est indécis et nécessite un examen complémentaire.

Démonstration

Soit \( (x_0, y_0) \) un point du domaine de \( f \), et considérons une courbe régulière \( \gamma(t) = (x(t), y(t)) \) contenue dans une courbe de niveau de \( f \).

Puisque la valeur de la fonction reste constante le long de cette courbe, sa dérivée directionnelle doit être nulle :

\[ f(x(t), y(t)) = \text{constante} \quad \Rightarrow \quad \frac{d}{dt} f(x(t), y(t)) = 0 \]

En appliquant la règle de la chaîne, on obtient :

\[ \frac{d}{dt} f(x(t), y(t)) = \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} = \nabla f \cdot \vec{v} = 0 \]

Ici, \( \vec{v} = \left( \frac{dx}{dt}, \frac{dy}{dt} \right) \) est le vecteur tangent à la courbe \( \gamma(t) \).

Comme \( \nabla f \cdot \vec{v} = 0 \), le gradient \( \nabla f \) est orthogonal au vecteur tangent : il est donc perpendiculaire à la courbe de niveau.

Et ainsi de suite.