Produit scalaire de deux vecteurs

Le produit scalaire (ou produit intérieur) de deux vecteurs est une opération qui associe un nombre réel (un scalaire) à la paire considérée. Il se définit comme le produit de la norme d’un vecteur par la norme de la projection du second sur le premier : $$ \vec{x} \cdot \vec{y} = | \vec{x} | \cdot | \vec{y} | \cdot \cos \theta $$ où θ est l’angle formé par les deux vecteurs. De manière équivalente, on peut l’exprimer comme la somme des produits des composantes correspondantes : \[ \vec{x} \cdot \vec{y} = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n \]

On parle aussi de produit intérieur, noté selon les cas <v₁, v₂>, (v₁, v₂) ou v₁•v₂.

Il faut rappeler que le produit scalaire <v₁, v₂> est toujours un nombre réel. Cela le distingue nettement du produit d’un vecteur par un scalaire k, qui produit un nouveau vecteur.

Pourquoi est-ce important ?

Le produit scalaire possède des propriétés géométriques fondamentales :

• Deux vecteurs orthogonaux (perpendiculaires) ont un produit scalaire nul.
  

  
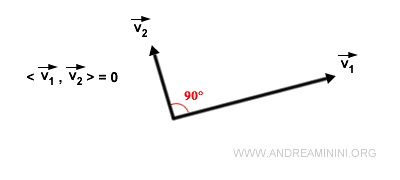
  En effet, le cosinus d’un angle droit vaut zéro. Ainsi, un produit scalaire nul indique que les vecteurs sont orthogonaux.

  Toutefois, un produit scalaire nul peut aussi provenir du fait que l’un des deux vecteurs (ou les deux) soit nul. Observations clés :
  
  
  • Le produit scalaire d’un vecteur avec lui-même est nul uniquement si ce vecteur est nul : $$ \langle \vec{v}, \vec{v} \rangle = 0 \ \Leftrightarrow \ \vec{v} = \{ \oslash \} $$
  • Pour un vecteur non nul, on a : $$ \langle \vec{v}, \vec{v} \rangle = |\vec{v}|^2 $$
• Si deux vecteurs sont parallèles ou colinéaires, leur produit scalaire est égal au produit de leurs normes. Cela découle du fait que cos(0°) = 1, donc <v₁, v₂> = |v₁₂|.
  
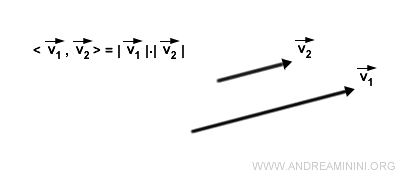
• Le produit scalaire sert aussi à calculer la norme d’un vecteur ou l’angle entre deux vecteurs.

Propriétés du produit scalaire. Ses principales propriétés sont résumées ci-dessous :

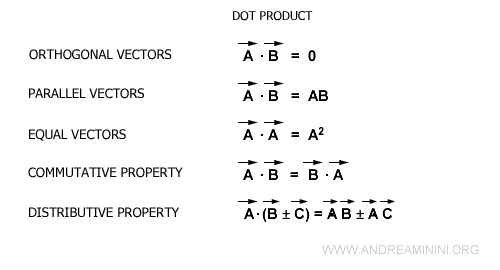
On notera que le produit scalaire avec le vecteur nul est toujours nul, puisque sa norme est nulle. Ainsi, un produit scalaire nul peut indiquer l’orthogonalité de deux vecteurs, mais ne le garantit pas.

Exemple pratique

Considérons deux vecteurs de l’espace bidimensionnel \( \mathbb{R}^2 \) :

$$ \vec{v_1} = \begin{pmatrix} 4 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Représentation graphique :

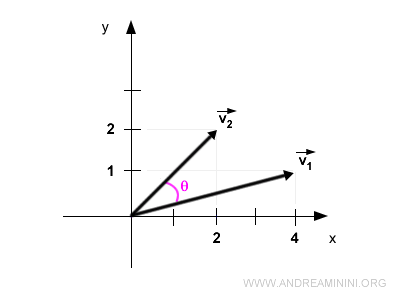
Ces vecteurs forment un angle θ = 30,96°.

Leur produit scalaire s’écrit :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = \vec{v_1} \cdot \vec{v_2} $$

En projetant orthogonalement v₂ sur v₁, on obtient un vecteur de norme |v₂| · cos θ, dirigé dans la même direction que v₁.

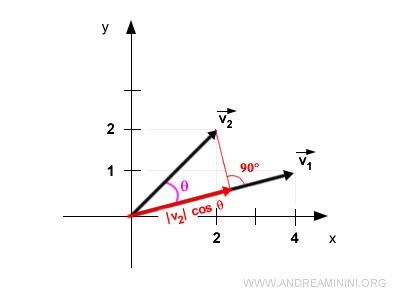
On a donc :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = |\vec{v_1}| \cdot \big(|\vec{v_2}| \cdot \cos \theta \big) $$

Avec |v₁| = 4,12 et |v₂| = 2,83 :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot (2,83 \cdot \cos \theta) $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot (2,83 \cdot \cos 30,96^\circ) $$

Or cos 30,96° = 0,86 :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot (2,83 \cdot 0,86) $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot 2,43 $$

Remarque. Le terme 2,83 · cos(30,96°) représente la norme de la projection de v₂ sur v₁, c’est-à-dire |v₂| · cos θ.

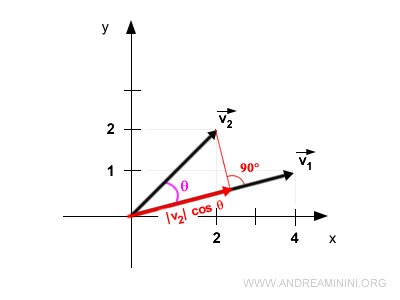
D’où :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot 2,43 $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 10 $$

Remarque. Le produit scalaire est commutatif : projeter v₁ sur v₂ conduit au même résultat.

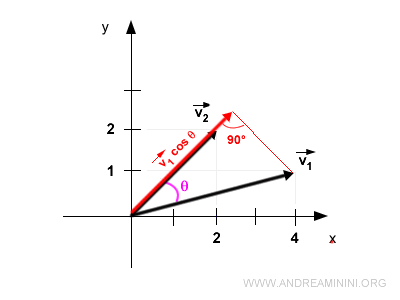
Calcul direct

On peut également le calculer directement grâce à la formule euclidienne :

$$ \langle \vec{v_1}, \vec{v_2} \rangle = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

Cette méthode est rapide et pratique : on multiplie les composantes correspondantes, puis on additionne les résultats.

 

 

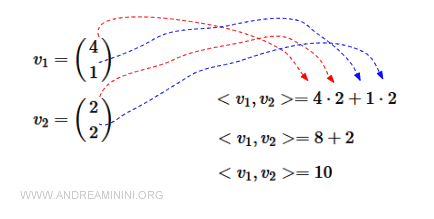
Dans notre exemple, les composantes en x sont 4 et 2, et les composantes en y sont 1 et 2.

On retrouve bien le même résultat que précédemment.

Propriétés du produit scalaire

Le produit scalaire de deux vecteurs d’un même espace vectoriel V sur le corps K = ℝ est une application bilinéaire et symétrique. Autrement dit, pour v₁ et v₂ :

$$ \langle \cdot, \cdot \rangle \:\: := \:\: V \times V \:\: \rightarrow \:\: \mathbb{R} $$

Produit scalaire euclidien

Parmi les différentes notions de produit scalaire, le produit scalaire euclidien est défini par : $$ \langle v_1 , v_2 \rangle = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

Exemple

Considérons deux vecteurs $v_1$ et $v_2$ dans $V = \mathbb{R}^3$ :

$$ v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

Leur produit scalaire euclidien est :

$$ \langle v_1 , v_2 \rangle = (2 \cdot 3) + ((-1) \cdot (-1)) + (1 \cdot 0) $$

$$ \langle v_1 , v_2 \rangle = 6 + 1 + 0 = 7 $$

Remarque. Le produit scalaire est dit non dégénéré : si $\langle w, v \rangle = 0$ pour tout $w \in V$, alors $v$ est nécessairement le vecteur nul.

Démonstration de la formule

Soient deux vecteurs $\vec{a}$ et $\vec{b}$. On écrit :

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z}, \quad \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Leur produit scalaire vaut :

$$ \vec{a} \cdot \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \cdot ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

En développant et en utilisant le fait que le produit scalaire de vecteurs unitaires orthogonaux est nul, tous les termes croisés disparaissent :

$$ \vec{u_x} \cdot \vec{u_y} = \vec{u_x} \cdot \vec{u_z} = \vec{u_y} \cdot \vec{u_z} = 0 $$

Il reste uniquement :

$$ a_x b_x (\vec{u_x} \cdot \vec{u_x}) + a_y b_y (\vec{u_y} \cdot \vec{u_y}) + a_z b_z (\vec{u_z} \cdot \vec{u_z}) $$

Or, pour tout vecteur $\vec{v}$, on a : $$ \vec{v} \cdot \vec{v} = ||\vec{v}||^2 $$ et comme les vecteurs unitaires ont une norme égale à 1 : $$ \vec{u_x} \cdot \vec{u_x} = \vec{u_y} \cdot \vec{u_y} = \vec{u_z} \cdot \vec{u_z} = 1 $$

D’où la formule finale :

$$ \vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z $$

Norme induite

Le produit scalaire induit naturellement une norme :

$$ ||v|| = \sqrt{ \langle v, v \rangle } $$

Cette norme est appelée norme euclidienne ou norme induite par le produit scalaire.

Exemple

Pour $v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}$ on obtient :

$$ || v_1 || = \sqrt{ (2 \cdot 2) + ((-1) \cdot (-1)) + (1 \cdot 1) } = \sqrt{6} $$

Inégalité de Cauchy-Schwarz

Pour tous vecteurs $v_1, v_2 \in V$, $$ |\langle v_1, v_2 \rangle| \le ||v_1|| \cdot ||v_2|| $$

L’égalité se produit si et seulement si les vecteurs sont linéairement dépendants.

Exemple

Avec $$ v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

on a : $$ |\langle v_1, v_2 \rangle| = 7, \quad ||v_1|| = \sqrt{6}, \quad ||v_2|| = \sqrt{10} $$

d’où : $$ 7 \le \sqrt{6} \cdot \sqrt{10} \approx 7,75 $$

L’inégalité est vérifiée, donc $v_1$ et $v_2$ ne sont pas dépendants.

Exemple 2

Si $$ v_1 = \begin{pmatrix} -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$

alors $$ \langle v_1, v_2 \rangle = -1 \cdot 1 + 1 \cdot -1 = -2 $$ et $$ ||v_1|| = ||v_2|| = \sqrt{2} $$

On obtient : $$ |\langle v_1, v_2 \rangle| = 2 = ||v_1|| \cdot ||v_2|| $$

On est bien dans le cas d’égalité, ce qui confirme la dépendance linéaire.

Remarques

• Contrairement au produit de réels, le produit scalaire peut être nul même si aucun vecteur n’est nul (par exemple s’ils sont perpendiculaires).
• S’ils ont même direction et même sens, le produit scalaire vaut le produit de leurs normes.
• S’ils sont colinéaires mais de sens opposé, le produit scalaire vaut l’opposé du produit de leurs normes.