Vecteurs

Qu’est-ce qu’un vecteur ?

Un vecteur est une notion mathématique fondamentale définie par trois caractéristiques essentielles : sa norme (ou longueur), sa direction et son sens.

Autrement dit, un vecteur est un segment auquel on attribue un sens de parcours : c’est donc un segment orienté.

Pour indiquer qu’il s’agit d’un vecteur, on note généralement ses extrémités en plaçant une flèche au-dessus (par exemple, \( \overrightarrow{AB} \)).

On peut aussi le représenter par une lettre minuscule surmontée d’une flèche (par exemple, \( \vec{v} \ )).

Le point de départ du vecteur est appelé le point d’application, et son extrémité, marquée par la pointe de la flèche, correspond au point terminal.

Le segment qui définit un vecteur indique sa direction, tandis que la flèche précise son sens.

Par exemple, dans un plan, un vecteur peut avoir une infinité de directions, correspondant aux droites passant par un point. Chaque direction admet deux sens opposés.

La longueur du segment orienté est appelée la norme du vecteur. Elle se note en encadrant le symbole du vecteur de barres verticales, par exemple : $ | \vec{v} | \ \ \text{ou} \ \ | \overrightarrow{AB} | $

Il arrive aussi que l’on note simplement la norme en écrivant la lettre du vecteur sans flèche (par exemple, \( v \)).

Remarque. Le symbole \( \vec{v} \) ne doit pas être confondu avec sa norme \( | \vec{v} | \). Le vecteur \( \vec{v} \) regroupe toutes ses caractéristiques (direction, sens, longueur) et constitue une grandeur vectorielle. Sa norme \( | \vec{v} | \), en revanche, n’indique que la longueur : c’est une grandeur scalaire (un nombre réel). La norme \( | \vec{v} | \) n’est donc qu’un aspect du vecteur \( \vec{v} \).

La norme d’un vecteur exprime l’intensité de la grandeur physique ou mathématique qu’il représente.

En d’autres termes, elle mesure « l’importance » du vecteur, indépendamment de sa direction.

En physique, par exemple, la norme d’un vecteur force traduit l’intensité de la force appliquée. En mathématiques, elle correspond à la distance à l’origine dans un espace vectoriel.

Pourquoi les vecteurs sont-ils essentiels ?

De nombreuses grandeurs physiques se définissent à la fois par leur norme, leur direction et leur sens.

On peut citer, par exemple, le déplacement, la vitesse, la force ou l’accélération.

Les vecteurs offrent une représentation graphique de ces grandeurs.

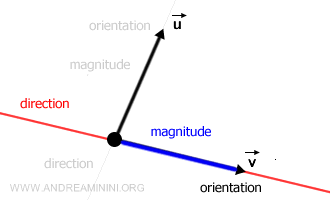
Chaque vecteur est défini de manière unique par sa direction, son sens et sa norme.

Pour le représenter visuellement, on utilise un segment orienté. Voici comment l’interpréter :

• La flèche indique le sens du vecteur.
• La longueur de la flèche (la norme) traduit son intensité et constitue une valeur scalaire.
• La droite qui supporte le vecteur détermine sa direction.

Vecteur et norme : ne pas confondre. Il est crucial de distinguer le vecteur de sa norme. Confondre les deux est une erreur fréquente et source de malentendus. Alors qu’un vecteur regroupe norme, direction et sens, sa norme n’est qu’une valeur scalaire correspondant à sa longueur. Deux vecteurs peuvent ainsi avoir la même norme mais différer par leur direction ou leur sens.

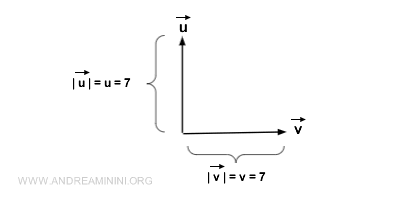
Par convention, la norme se note soit par le symbole du vecteur sans flèche, soit en plaçant ce symbole entre barres verticales. Les vecteurs, eux, sont généralement notés par une lettre surmontée d’une flèche ou écrite en gras.

Bien que l’étude des vecteurs puisse être très vaste, leur principe de base reste simple et constant.

Opérations sur les vecteurs

Les vecteurs se prêtent à deux opérations fondamentales :

• Addition vectorielle
  La somme de deux vecteurs donne un troisième vecteur, appelé le résultant.
  
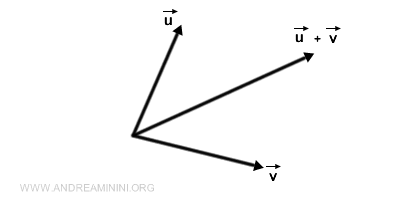
• Multiplication par un scalaire
  Multiplier un vecteur par un scalaire (par exemple 2) revient à obtenir un vecteur dont la norme est multipliée par ce facteur, tout en conservant la même direction et le même sens.
  

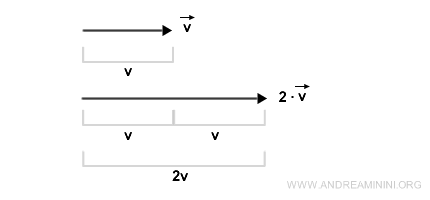
Dans les deux cas, le résultat est encore un vecteur.

Qu’est-ce qu’un vecteur ?

Les vecteurs occupent une place centrale en mathématiques et en physique. Pour bien en saisir l’intuition, commençons par les examiner dans un plan à deux dimensions.

Dans le plan (x,y), un vecteur est défini comme un segment orienté. Ce segment se caractérise par trois attributs principaux : sa norme (ou longueur), sa direction et son sens.

Voici une illustration :

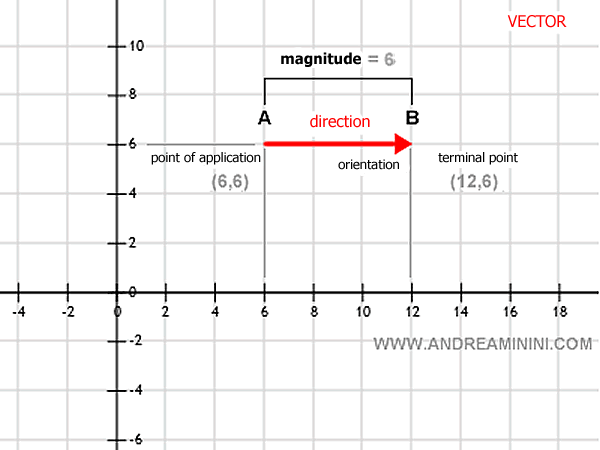
Exemple. Considérons dans un plan un segment de longueur 6 unités, allant du point A (6,6) au point B (12,6). En choisissant le sens de A vers B, on définit un vecteur.

En mathématiques et en physique, on note les vecteurs à l’aide de leurs points initial et terminal avec une flèche :

$$ \overrightarrow{AB} $$

Ou, plus simplement :

$$ AB $$

Vecteurs liés et vecteurs libres

Vecteurs liés

Un vecteur lié possède un point de départ fixé, appelé point d’application.

Par exemple, pour un point P et une origine O dans le plan, le vecteur allant de O vers P se note : $$ \overrightarrow{OP} $$. On peut aussi le désigner par une lettre minuscule comme v, u ou w.

Illustration :

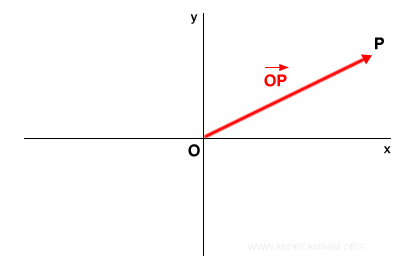
L’ensemble des vecteurs ayant le même point de départ, disons O, se note :

$$ V^2(O) $$

Représentation pratique :

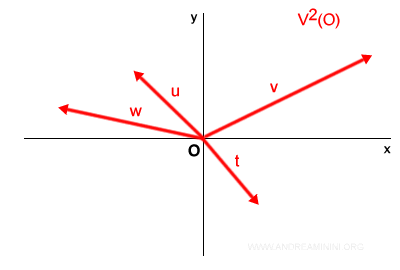
Il faut noter que, même si O désigne souvent l’origine du plan, le point de départ d’un vecteur peut être différent.

Par exemple, le segment orienté AB a pour point initial A.

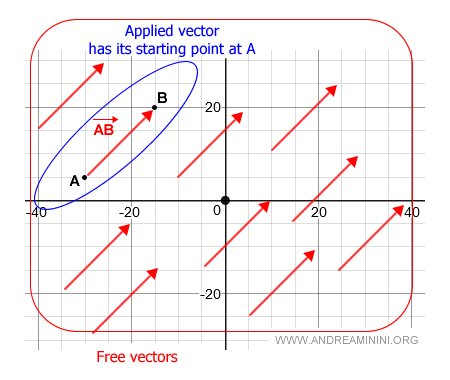
Vecteurs libres

Un vecteur, au sens général, est l’ensemble de tous les segments orientés parallèles, de même direction et de même norme.

Contrairement au vecteur lié, le vecteur libre n’a pas de point d’application fixé. Il est défini uniquement par sa direction et sa norme.

L’ensemble de ces vecteurs dans un plan se note :

$$ V $$

Si le point d’application n’est pas précisé, il s’agit d’un vecteur libre, c’est-à-dire de la classe de tous les vecteurs équivalents.

Remarque. Un vecteur libre regroupe tous les vecteurs d’une même classe d’équivalence et en constitue le représentant.

Définir un vecteur en mathématiques

Un vecteur est un élément d’un espace vectoriel. Dans le cadre des espaces vectoriels réels, un vecteur est une n-uplet ordonnée de nombres réels ( x₁, … , x_n ).

Les nombres réels qui composent un vecteur s’appellent ses composantes.

Un exemple concret

Voici quelques exemples de vecteurs à deux composantes (n=2) à valeurs réelles :

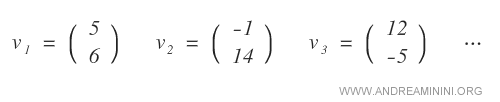
L’ensemble de tous les vecteurs à deux composantes constitue l’espace vectoriel réel ( R² = R�-R ).

Cet espace ( R² ) correspond à l’ensemble des points du plan cartésien.

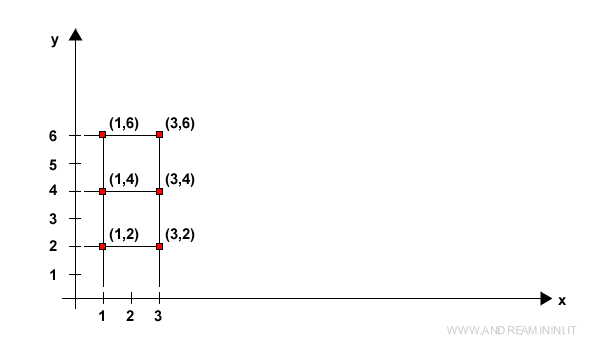
En effet, chaque paire de réels ( x₁, x₂ ) correspond à un point unique ( x, y ) du plan cartésien.

Addition de vecteurs

Étant donnés deux vecteurs numériques à n composantes :

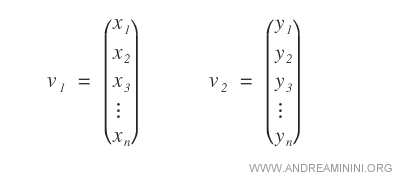
La somme de ces vecteurs est un vecteur à n composantes, dont chaque composante ( z_n ) est la somme des composantes correspondantes ( x_n + y_n ).

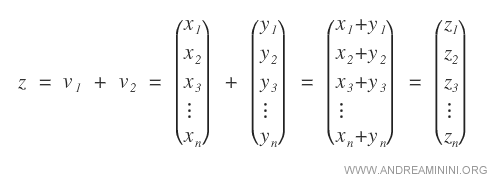
Multiplication d’un vecteur par un scalaire

Étant donné un vecteur v à n composantes et un scalaire réel quelconque α, le produit du vecteur par ce scalaire est un vecteur dont chaque composante x_n est multipliée par α.

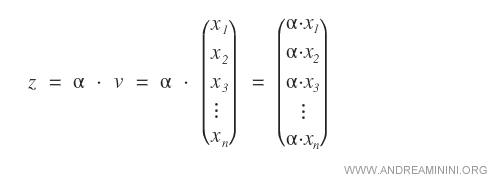
Représentation des vecteurs

Dans un espace bidimensionnel, on peut représenter les vecteurs sur le plan cartésien.

Deux vecteurs géométriques OE₁ et OE₂ sont linéairement indépendants s’ils appartiennent à deux droites distinctes passant par l’origine.

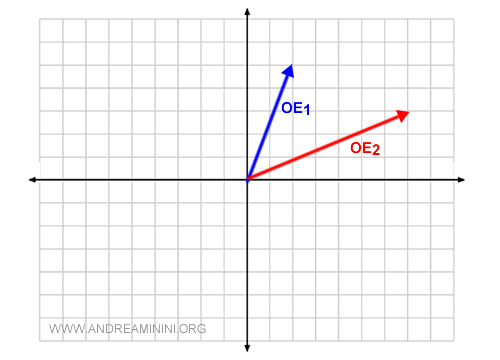
Deux vecteurs indépendants forment une base de l’espace vectoriel V²O, car leurs combinaisons linéaires engendrent tous les vecteurs libres de l’espace bidimensionnel V².

$$ B = \{ OE_1 , OE_2 \} $$

À chaque point P du plan, on associe un vecteur numérique v(x,y) qui fournit les coordonnées C_v(x,y) du vecteur OP relativement à la base { OE₁, OE₂ }.

$$ OP = a_1 \cdot OE1 + a_2 \cdot OE2 $$

Réciproquement, tout vecteur v(x,y) correspond à un point P du plan par combinaison linéaire.

Il existe donc une correspondance biunivoque entre les vecteurs de l’espace \( \mathbb{R}^2 \) et les points \( (x, y) \) du plan.

Exemple pratique

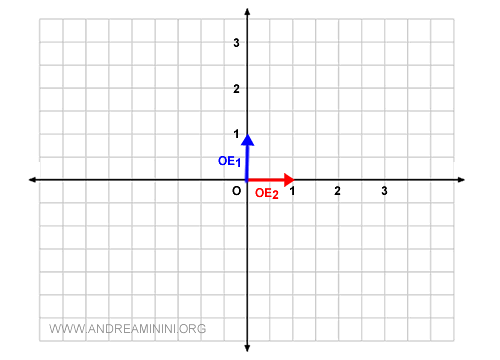
J’utilise les vecteurs v₁=(0,1) et v₂(1,0) comme base vectorielle B, correspondant respectivement à OE₁ et OE₂.

$$ B = \{ v_1 , v_2 \} \\ v_1 = \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ v_2 = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

Outre leur indépendance linéaire, v₁ et v₂ sont orthogonaux, ce qui facilite la représentation graphique.

Je place maintenant le point P sur la figure.

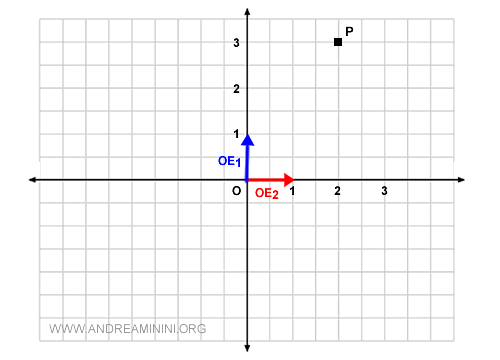
Comme tout point du plan, P est associé à un vecteur passant par l’origine (O).

Ici, il s’agit du vecteur géométrique OP.

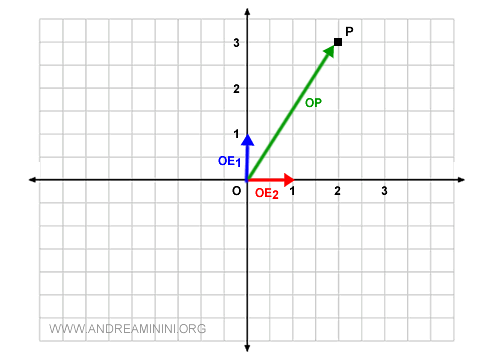
Le vecteur \( OP \) est linéairement dépendant de la base { OE₁, OE₂ } puisqu’on peut l’exprimer comme combinaison linéaire de ces vecteurs.

Autrement dit, il existe deux scalaires c₁ et c₂, appelés coordonnées, tels que :

$$ \overrightarrow{OP} = c_1 OE_1 + c_2OE_2$$

$$ \overrightarrow{OP} = c_1 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + c_2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = 3 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + 2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 0 \\ 3 \end{pmatrix} + \begin {pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 2 \\ 3 \end{pmatrix} $$

Le calcul est ici immédiat.

Les coordonnées sont c₁=3 et c₂=2, c’est-à-dire trois fois OE₁ et deux fois OE₂.

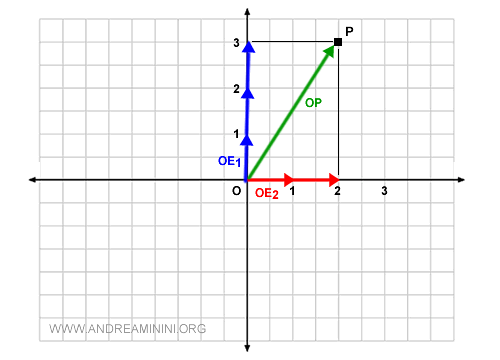
La correspondance entre le point P et le vecteur OP se note par la relation d’équivalence :

$$ \overrightarrow{OP} \equiv P \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

De la même manière, on peut représenter n’importe quel autre point du plan cartésien R �- R, ou R².

Remarque. Cette correspondance entre points et vecteurs est précieuse, car elle permet d’étudier des propriétés géométriques via l’algèbre linéaire.

Vecteurs dans des espaces multidimensionnels

En mathématiques, les vecteurs ne se limitent pas au plan à deux dimensions que l’on visualise le plus aisément. Ils existent et se définissent dans des espaces de dimension quelconque.

Vecteurs bidimensionnels

Dans un espace à deux dimensions, noté R², un vecteur est caractérisé par la différence entre ses points initial et terminal dans le plan.

$$ V \{ x_2-x_1, y_2-y_1 \} $$

Exemple

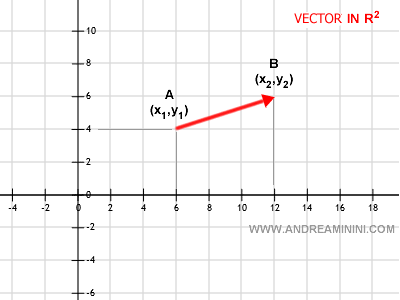
Considérons un vecteur dans le plan : $$ V \{ x_2-x_1, y_2-y_1 \} $$. En détaillant : $$ V \{ 12-6, 6-4 \} $$ on obtient : $$ V \{ 6, 2 \} $$

 

Vecteurs tridimensionnels

Dans un espace à trois dimensions, R³, l’écriture algébrique est analogue, avec l’ajout de la coordonnée z.

$$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$

Par concision, on note parfois directement les composantes (c’est-à-dire ces différences) :

$$ V \{ x, y, z \} $$

Où :

$$ x=x_2-x_1 $$ $$ y=y_2-y_1 $$ $$ z=z_2-z_1 $$

Cette notation devient particulièrement pratique dès que l’on passe à des dimensions supérieures.

Exemple

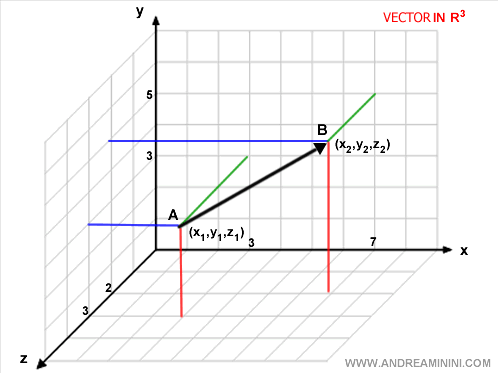
Considérons un vecteur dans l’espace 3D (x,y,z) : $$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$. Pour A=(3,3,3) et B=(7,5,2) : $$ V \{ 7-3, 5-3, 2-3 \} $$ ce qui donne : $$ V \{ 4, 2, -1 \} $$

Vecteurs en dimension n

En généralisant à un espace de dimension n, noté Rⁿ, on écrit :

$$ V \{ x_1, x_2, \ldots , x_n \} $$

La représentation géométrique devient toutefois délicate au-delà de trois dimensions.

Notre intuition est ancrée dans trois dimensions, la quatrième étant souvent pensée comme le temps. Au-delà, l’intuition géométrique atteint vite ses limites. Ce n’est pas une faiblesse, mais le reflet de la complexité de ces espaces. Pour les étudier, on recourt à l’abstraction algébrique ou à d’autres modes de représentation.

Ainsi, en dimension n, un vecteur se décrit généralement comme une n-uplet ordonnée de n éléments :

$$ V \{ x_1, x_2, \ldots , x_n \} $$

Chaque élément, de x₁ à x_n, peut être un nombre réel quelconque.

Par exemple

$$ V \{ 4, 2, -1, 7 , 3 \} $$

L’étude des vecteurs multidimensionnels constitue l’un des piliers de l’algèbre linéaire.