Équations vectorielle, paramétriques et cartésienne d’un plan

Un plan est défini par deux vecteurs géométriques linéairement indépendants, qui déterminent deux directions distinctes, ainsi que par un point appartenant à ce plan.

$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

$$ P_0 = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Si le point P₀ n’est pas précisé, les deux vecteurs v₁ et v₂ décrivent l’ensemble des plans parallèles aux directions données, mais ils ne suffisent pas à définir un plan unique.

Dès lors, tout point du plan peut s’exprimer au moyen de l’équation vectorielle du plan :

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

De cette équation vectorielle, on déduit immédiatement les équations paramétriques du plan :

$$ \begin{cases} x = x_0 + t_1 \cdot l_1 + t_2 \cdot l_2 \\ y = y_0 + t_1 \cdot m_1 + t_2 \cdot m_2 \\ z = z_0 + t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

Ces équations peuvent également être réécrites sous la forme :

$$ \begin{cases} x - x_0 = t_1 \cdot l_1 + t_2 \cdot l_2 \\ y - y_0 = t_1 \cdot m_1 + t_2 \cdot m_2 \\ z - z_0 = t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

On obtient ainsi trois vecteurs : P₀P, v₁ et v₂, que l’on peut disposer dans une matrice carrée :

$$ \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} $$

Le calcul du déterminant de cette matrice fournit l’équation cartésienne du plan :

$$ det \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} = $$

$$ (x-x_0) \cdot det \begin{pmatrix} m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} + (y-y_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ n_1 & n_2 \end{pmatrix} + (z-z_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} $$

Un exemple concret

Considérons deux vecteurs directeurs :

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

et un point :

$$ P = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

Vérifions d’abord si ces deux vecteurs sont linéairement indépendants.

Leur rang est égal à deux, ce qui prouve qu’ils sont bien linéairement indépendants.

$$ r_k = \begin{pmatrix} 3 & 4 \\ 1 & 3 \\ 2 & 1 \end{pmatrix} = 2 $$

Remarque. Lorsque le rang est égal au nombre de vecteurs considérés, ceux-ci sont linéairement indépendants.

Vérifions maintenant si le point P appartient au plan.

Déterminer si un point appartient à un plan

Pour que le point P soit situé dans le plan, il doit exister deux paramètres t₁ et t₂ tels que la relation suivante soit satisfaite :

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 v_1 + t_2 v_2 $$

En remplaçant les vecteurs directeurs, on obtient :

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Choisissons comme point de référence P₀ un point du plan, par exemple l’extrémité d’un des vecteurs :

$$ \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$

L’équation devient alors :

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

En substituant (x, y, z) par les coordonnées du point (10,5,5), on obtient le système suivant :

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Ce système est compatible.

En choisissant t₁=1 et t₂=1, on obtient bien le point (10,5,5).

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 + 3 + 4 \\ 1 + 1 + 3 \\ 2 + 2 + 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

On peut donc écrire l’équation vectorielle du plan sous la forme :

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Autre méthode de vérification. Pour confirmer l’existence d’une solution, on peut reformuler l’équation vectorielle ainsi : $$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 7 \\ 4 \\ 3 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ En disposant les vecteurs des coefficients dans une matrice colonne : $$ \begin{pmatrix} 7 & 3 & 4 \\ 4 & 1 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ Si le rang de cette matrice est inférieur au nombre de vecteurs (c’est-à-dire strictement inférieur à trois), les vecteurs sont dépendants et le système admet une solution. Ici, le rang est 2 (r_k=2), donc le système a bien une solution. L’interprétation est claire : les vecteurs v₁(3,1,2) et v₂(4,3,1) sont indépendants, et pour que le vecteur (7,4,3) appartienne au plan, il doit être une combinaison linéaire de v₁ et v₂.

Une fois l’équation vectorielle établie, il est immédiat d’en déduire la paramétrisation du plan :

$$ \begin{cases} x = 10 + 3t_1 + 4t_2 \\ y = 5 + t_1 + 3t_2 \\ z = 5 + 2t_1 + t_2 \end{cases} $$

Enfin, pour obtenir l’équation cartésienne du plan, on peut réorganiser l’équation vectorielle de la manière suivante :

$$ \begin{pmatrix} x - 10 \\ y - 5 \\ z - 5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Soit la matrice :

$$ \begin{pmatrix} x - 10 & 3 & 4 \\ y - 5 & 1 & 3 \\ z - 5 & 2 & 1 \end{pmatrix} $$

Le déterminant de cette matrice fournit directement l’équation cartésienne du plan.

On a ainsi obtenu l’équation cartésienne du plan.

Représentation graphique du plan dans un espace tridimensionnel :

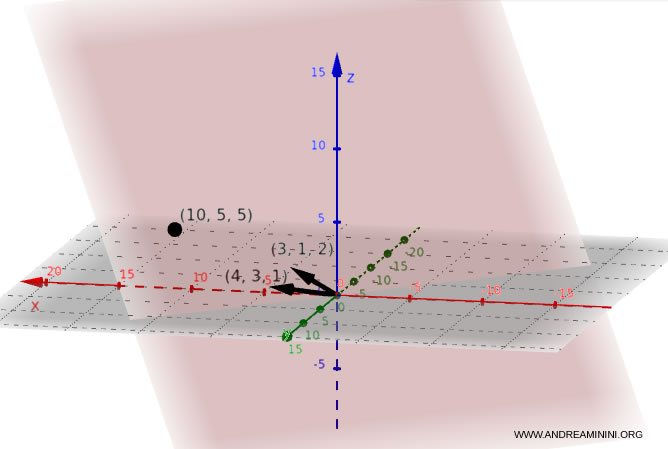
Conversion de l’équation cartésienne en équation paramétrique d’un plan

Examinons à présent le processus inverse : à partir de l’équation cartésienne d’un plan, il s’agit d’en déduire l’équation paramétrique.

L’équation cartésienne du plan s’écrit :

$$ ax + by + cz + d = 0 $$

L’équation vectorielle-paramétrique correspondante est de la forme :

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

Les coefficients a, b et c de l’équation cartésienne définissent le vecteur normal au plan, c’est-à-dire un vecteur perpendiculaire à celui-ci :

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

Un vecteur normal étant perpendiculaire au plan, il l’est nécessairement à tout vecteur contenu dans le plan.

Autrement dit, le vecteur normal est orthogonal aux vecteurs directeurs qui interviennent dans l’équation paramétrique.

Il en découle que le produit scalaire du vecteur normal avec chacun des vecteurs directeurs doit être nul :

$$ \langle n , v_2 \rangle = 0 \qquad \langle n , v_1 \rangle = 0 $$

Cette condition permet de déterminer deux vecteurs linéairement indépendants, orthogonaux au vecteur normal, à partir desquels on construit l’équation vectorielle (ou paramétrique) du plan.

Exemple

Considérons l’équation cartésienne suivante :

$$ -5x -y + 8z + 15 = 0 $$

Le vecteur normal associé est :

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

Ce vecteur est orthogonal au plan défini par l’équation cartésienne, et par conséquent à tout vecteur non nul contenu dans ce plan.

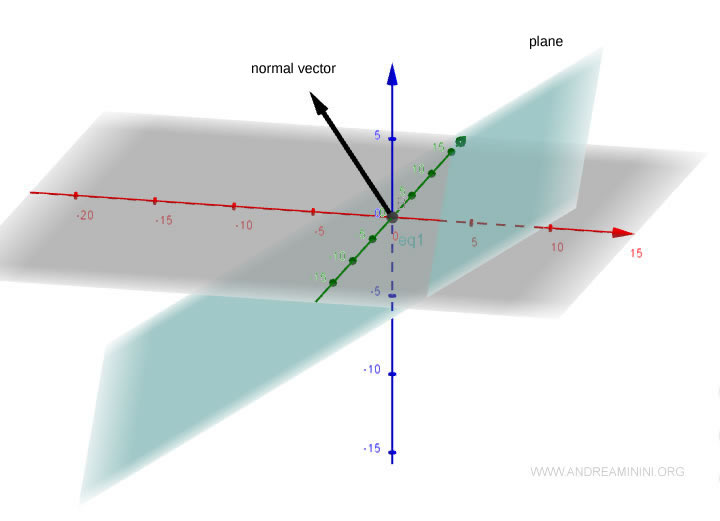
Il nous faut maintenant déterminer deux vecteurs linéairement indépendants et orthogonaux au vecteur normal.

La méthode consiste à annuler l’une des composantes du vecteur normal, à inverser les deux autres puis à changer le signe de l’une d’entre elles.

En annulant par exemple la composante x du vecteur normal :

$$ \begin{pmatrix} 0 \\ -1 \\ 8 \end{pmatrix} $$

On inverse les deux dernières composantes :

$$ \begin{pmatrix} 0 \\ 8 \\ -1 \end{pmatrix} $$

Puis on change le signe de l’une d’elles, ce qui fournit le premier vecteur directeur :

$$ v_1 = \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} $$

En appliquant le même procédé en annulant cette fois la composante y :

$$ \begin{pmatrix} -5 \\ 0 \\ 8 \end{pmatrix} $$

et après inversion et changement de signe, on obtient le second vecteur directeur :

$$ v_2 = \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

Nous avons ainsi construit deux vecteurs orthogonaux au vecteur normal.

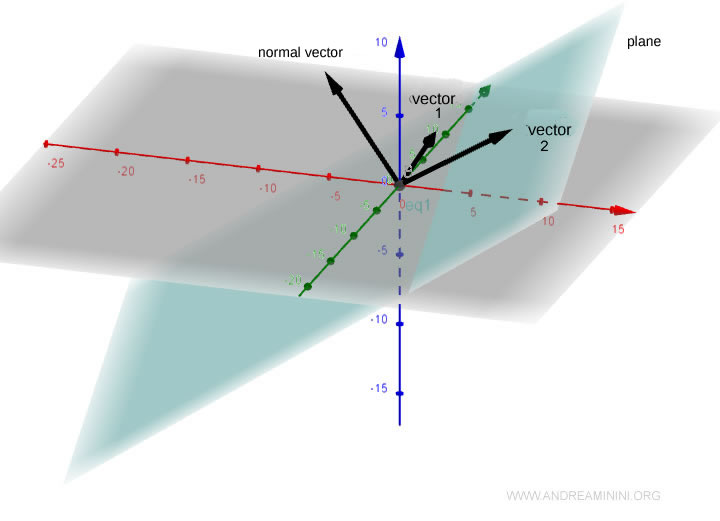
Vérifions qu’ils sont bien linéairement indépendants :

$$ r_k \begin{pmatrix} 0 & 8 \\ 8 & 0 \\ 1 & 5 \end{pmatrix} = 2 $$

Le rang de la matrice formée par ces vecteurs est égal à 2, c’est-à-dire au nombre de vecteurs. Ils sont donc linéairement indépendants.

Vérifions également leur orthogonalité au vecteur normal :

$$ \langle n , v_1 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} \rangle = 0 $$

$$ \langle n , v_2 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} \rangle = 0 $$

Les produits scalaires étant nuls, v₁ et v₂ sont bien orthogonaux au vecteur normal, et peuvent servir de vecteurs directeurs du plan.

On peut alors écrire l’équation vectorielle du plan :

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

Cette équation décrit le plan ainsi que tous les plans parallèles.

Pour obtenir l’équation du plan spécifique considéré, il suffit d’ajouter un point P₀ appartenant au plan.

Par exemple, en posant x = 0 et z = 0 dans l’équation cartésienne, on calcule y :

$$ -5x -y + 8z + 15 = 0 \\ -5(0) -y + 8(0) + 15 = 0 \\ y = 15 $$

On obtient ainsi un point du plan : P(0, 15, 0).

En remplaçant ce point dans l’équation vectorielle, on obtient l’équation vectorielle du plan :

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 15 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

À partir de là, on déduit aisément l’équation paramétrique du plan :

$$ \begin{cases} x = 8t_2 \\ y = 15 + 8t_1 \\ z = t_1 + 5t_2 \end{cases} $$

Retrouver l’équation cartésienne à partir du vecteur normal

Reprenons l’équation cartésienne :

$$ -5x -y + 8z + 15 = 0 $$

Le vecteur normal correspondant est :

$$ n = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

Ce vecteur est orthogonal au plan cartésien.

Sélectionnons un point particulier du plan.

En posant y = 0 et z = 0, on obtient la coordonnée x :

$$ -5x -y + 8z + 15 = 0 $$

$$ -5x + 15 = 0 $$

$$ x = 15 $$

On obtient donc un point du plan :

$$ P_1 = \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} $$

Considérons un point générique du plan :

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

Le vecteur reliant P₁ à P est :

$$ P_1P = \begin{pmatrix} x - 15 \\ y \\ z \end{pmatrix} $$

Ce vecteur appartient au plan.

Tout vecteur du plan étant orthogonal au vecteur normal, on doit avoir :

$$ \langle P_1P , n \rangle = 0 $$

En développant le produit scalaire :

$$ \left\langle \begin{pmatrix} x - 15 \\ y \\ z \end{pmatrix} , \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} \right\rangle = -5(x - 15) - y + 8z = 0 $$

$$ -5x + 75 - y + 8z = 0 $$

On retrouve ainsi l’équation cartésienne du plan, ce qui confirme la cohérence de la démarche.