Plans parallèles, confondus et sécants dans l’espace
Dans $ \mathbb{R}^3 $, deux plans peuvent être parallèles, confondus ou sécants.
- Ils sont parallèles s’ils n’ont aucun point commun.
- Ils sont confondus lorsqu’ils coïncident entièrement, c’est-à-dire qu’ils possèdent exactement les mêmes points.
- Ils sont sécants lorsqu’ils partagent une infinité de points, tous situés sur leur droite d’intersection.
En résumé, si deux plans se coupent, leur intersection est nécessairement une droite. S’ils sont parallèles ou confondus, l’intersection est soit vide, soit l’ensemble du plan lui-même.
Remarque : Deux plans parallèles ou confondus possèdent des vecteurs normaux colinéaires. Ils diffèrent uniquement par leur position relative. À l’inverse, deux plans sécants se rencontrent selon une droite et leurs vecteurs normaux ne sont pas parallèles.
Détermination de la position relative de deux plans
Pour savoir si deux plans sont parallèles, confondus ou sécants, on examine la dépendance linéaire des vecteurs directeurs associés à leurs équations paramétriques.
- Si les vecteurs sont linéairement dépendants, les plans sont parallèles ou confondus.
- Si les vecteurs sont linéairement indépendants, les plans sont nécessairement sécants.
Vérification de la dépendance linéaire
Soient deux plans donnés sous forme paramétrique :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} x'_0 \\ y'_0 \\ z'_0 \end{pmatrix} + t_1 \begin{pmatrix} l_3 \\ m_3 \\ n_3 \end{pmatrix} + t_2 \begin{pmatrix} l_4 \\ m_4 \\ n_4 \end{pmatrix} $$
On place les quatre vecteurs directeurs en colonnes dans une matrice :
$$ \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} $$
Le rang de cette matrice permet de conclure :
- Si $r_k \leq 2$, les vecteurs sont dépendants et les plans sont parallèles ou confondus. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} \le 2 $$
Astuce : Pour distinguer ces deux cas, il suffit de tester si un point d’un plan appartient aussi à l’autre. Si oui, les plans sont confondus ; sinon, ils sont parallèles distincts.
- Si $r_k = 3$, les vecteurs sont indépendants et les plans sont sécants. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} = 3 $$
On peut résumer la règle, dans le cas paramétrique, par le tableau suivant :
| Rang de la matrice | Relation entre les vecteurs | Position relative des plans |
|---|---|---|
| 1 - 2 | Dépendants | Plans parallèles ou confondus |
| 3 | Indépendants | Plans sécants (intersection : une droite) |
Cas des équations cartésiennes
Soient deux plans définis par :
$$ a_1 x + b_1 y + c_1 z + d_1 = 0 $$
$$ a_2 x + b_2 y + c_2 z + d_2 = 0 $$
Leurs vecteurs normaux sont linéairement dépendants si le rang de la matrice des coefficients est $1$ :
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 1 $$
Dans ce cas, les plans sont parallèles ou confondus.
Les vecteurs sont indépendants si le rang est $2$ :
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 2 $$
Les plans sont alors nécessairement sécants.
On peut résumer la règle dans le cas cartésien ainsi :
| Rang de la matrice | Relation entre les vecteurs | Position relative des plans |
|---|---|---|
| 1 | Dépendants | Plans parallèles ou confondus |
| 2 | Indépendants | Plans sécants (intersection : une droite) |
Exemples
Exemple 1 (équations paramétriques)
Considérons deux plans de l’espace :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
On regroupe les vecteurs directeurs dans une matrice et l’on calcule son rang :
$$ r_k \begin{pmatrix} 0 & 2 & 0 & 1 \\ -1 & -1 & -3 & -1 \\ 2 & 0 & 6 & 1 \end{pmatrix} = 2 $$
Comme le rang est égal à 2, les vecteurs sont linéairement dépendants. Les deux plans sont donc soit parallèles, soit confondus.
Comment les distinguer ?
Il suffit de vérifier si un point de l’un des plans appartient aussi à l’autre.
On sait que le point $P(0,0,0)$ appartient au premier plan. Substituons-le dans l’équation du second :
$$ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Ce qui revient au système :
$$ \begin{cases} t_2 = 0 \\ 1 - 3t_1 = 0 \\ 6t_1 = 0 \end{cases} $$
Ce système est contradictoire, car il impose deux valeurs incompatibles pour $t_1$. Par conséquent, le point $P(0,0,0)$ n’appartient pas au second plan. Les plans ne sont donc pas confondus, mais bien parallèles.
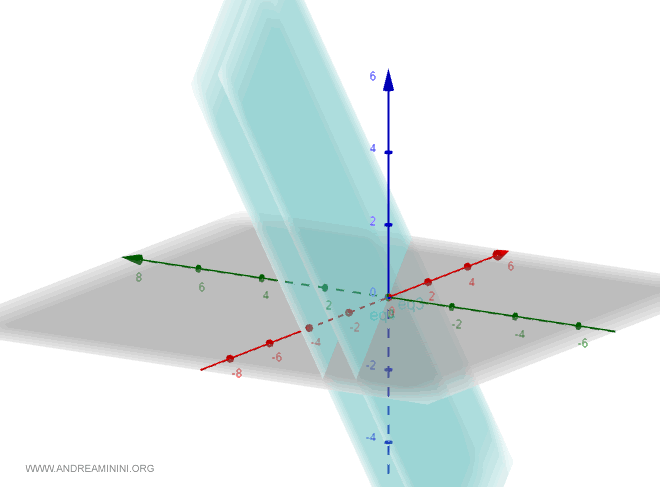
Exemple 2 (équations cartésiennes)
Examinons maintenant deux plans définis par :
$$ x + 2y + z = 0 $$
$$ 2x + 4y + 2z - 5 = 0 $$
Leurs coefficients s’écrivent dans la matrice :
$$ \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} $$
Le rang vaut :
$$ r_k \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} = 1 $$
Les vecteurs normaux sont donc dépendants, ce qui indique que les plans sont parallèles ou confondus.
Comment trancher ?
Choisissons un point sur le premier plan en fixant $x = 0$ et $y = 0$ :
$$ z = 0 $$
On obtient $P(0,0,0)$.
Vérifions dans la seconde équation :
$$ 2(0) + 4(0) + 2(0) - 5 = -5 \neq 0 $$
Le point n’appartient pas au second plan, ce qui exclut le cas de plans confondus. Ils sont donc parallèles.
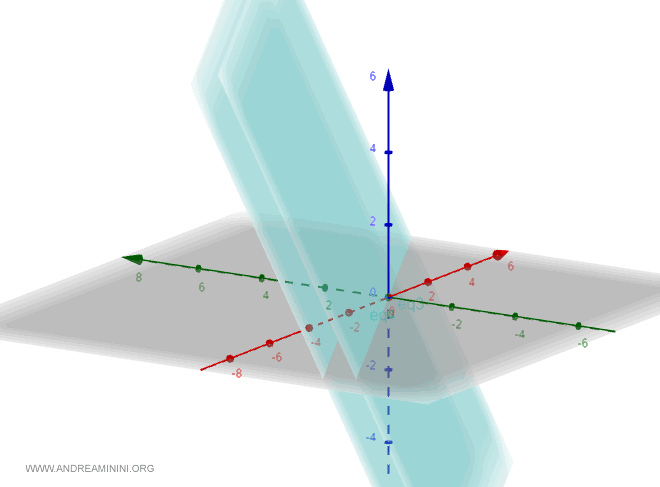
Remarques complémentaires
- Théorème de la droite perpendiculaire à deux plans
Si deux plans $ \alpha $ et $ \beta $ sont perpendiculaires à une même droite $r$ en deux points distincts $P$ et $Q$, alors ils sont nécessairement parallèles.
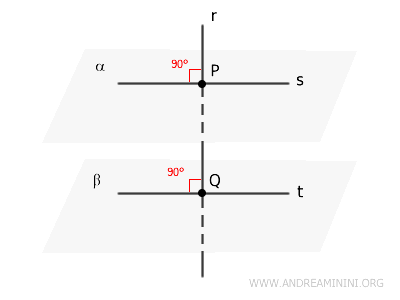
- Théorème des plans parallèles coupés par un troisième plan
Lorsqu’un plan $ \pi $ coupe deux plans parallèles $ \pi_1 $ et $ \pi_2 $, les droites d’intersection obtenues sont parallèles.
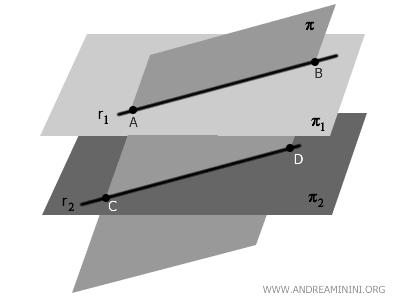
Cela tient au fait que $ \pi_1 $ et $ \pi_2 $ sont parallèles et équidistants : en les coupant selon le même angle, le plan $ \pi $ engendre deux droites $r_1$ et $r_2$, qui sont forcément parallèles.
Et ainsi de suite.