Forma de Interceptos de la Ecuación de un Plano
La forma de interceptos de la ecuación de un plano se obtiene determinando los valores de p, q y r, de modo que la ecuación cartesiana adopte la siguiente expresión:
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
La ecuación cartesiana general del plano es:
$$ ax+by+cz+d=0 $$
Si igualamos a cero las variables y y z, se obtiene:
$$ ax+d=0 \\ ax=-d \\ x=-\frac{d}{a} $$
Si igualamos a cero las variables x y z, se obtiene:
$$ by+d=0 \\ by=-d \\ y=-\frac{d}{b} $$
Si igualamos a cero las variables x e y, se obtiene:
$$ cz+d=0 \\ cz=-d \\ z=-\frac{d}{c} $$
Estos valores calculados se asignan a los coeficientes p, q y r:
$$ p = -\frac{d}{a} $$
$$ q = -\frac{d}{b} $$
$$ r = -\frac{d}{c} $$
Por tanto, se obtiene la forma de interceptos de la ecuación del plano:
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
¿Para qué sirve la forma de interceptos de la ecuación de un plano?
Los valores p, q y r indican los puntos donde el plano corta a los ejes coordenados:
- p = intersección con el eje x
- q = intersección con el eje y
- r = intersección con el eje z
Ejemplo Práctico
Consideremos un plano definido por la siguiente ecuación cartesiana:
$$ -5x - y + 8z + 15 = 0 $$
Igualando y = z = 0, obtenemos el punto de intersección sobre el eje x:
$$ -5x + 15 = 0 \\ x = \frac{15}{5} \\ x = 3 $$
Igualando x = z = 0, obtenemos el punto de intersección sobre el eje y:
$$ -y + 15 = 0 \\ -y = -15 \\ y = 15 $$
Igualando x = y = 0, obtenemos el punto de intersección sobre el eje z:
$$ 8z + 15 = 0 \\ 8z = -15 \\ z = -\frac{15}{8} $$
Así, los valores de p, q y r en la forma de interceptos son:
$$ p = 3 $$
$$ q = 15 $$
$$ r = -\frac{15}{8} $$
Por lo tanto, la forma de interceptos de la ecuación del plano es:
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
$$ \frac{x}{3} + \frac{y}{15} + \frac{z}{-\frac{15}{8}} = 1 $$
En esta forma, los denominadores representan exactamente las distancias desde el origen hasta los puntos donde el plano corta los ejes coordenados (x, y, z).
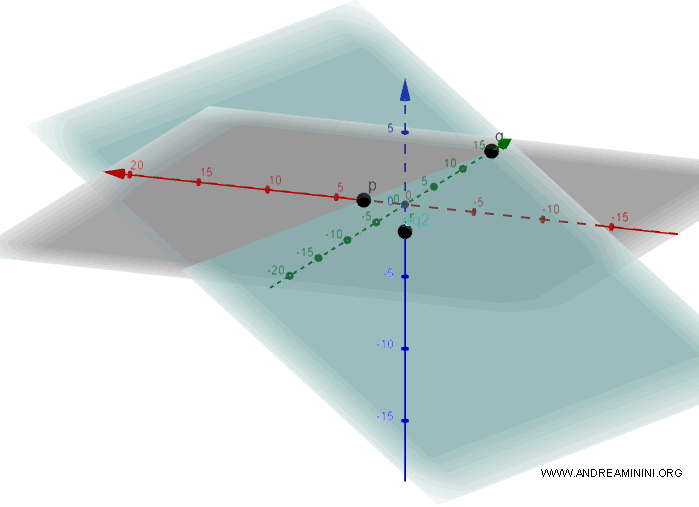
Nota: Representación gráfica del plano y de sus puntos de intersección p, q y r.