Ecuaciones vectorial, paramétricas y cartesiana de un plano

Un plano queda determinado por dos vectores geométricos linealmente independientes, que definen direcciones distintas, y un punto que pertenece al plano.

$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

$$ P_0 = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Si no se especifica el punto P₀, los dos vectores geométricos v₁ y v₂ describen todos los planos paralelos a dichas direcciones, pero no determinan un plano concreto.

Por ello, todo punto del plano se puede expresar mediante la siguiente ecuación vectorial del plano.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

A partir de la ecuación vectorial, se derivan de forma inmediata las ecuaciones paramétricas del plano.

$$ \begin{cases} x = x_0 + t_1 \cdot l_1 + t_2 \cdot l_2 \\ y = y_0 + t_1 \cdot m_1 + t_2 \cdot m_2 \\ z = z_0 + t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

Estas ecuaciones también pueden reescribirse así:

$$ \begin{cases} x - x_0 = t_1 \cdot l_1 + t_2 \cdot l_2 \\ y - y_0 = t_1 \cdot m_1 + t_2 \cdot m_2 \\ z - z_0 = t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

De este modo, se obtienen tres vectores: P₀P, v₁ y v₂, que se pueden organizar en una matriz cuadrada.

$$ \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} $$

El cálculo del determinante de esta matriz proporciona la ecuación cartesiana del plano.

$$ det \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} = $$

$$ (x-x_0) \cdot det \begin{pmatrix} m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} + (y-y_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ n_1 & n_2 \end{pmatrix} + (z-z_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} $$

Un ejemplo práctico

Dispongo de dos vectores directores:

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

y de un punto:

$$ P = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

Voy a comprobar si estos dos vectores son linealmente independientes.

El rango de los vectores es igual a dos. Por lo tanto, son linealmente independientes.

$$ r_k = \begin{pmatrix} 3 & 4 \\ 1 & 3 \\ 2 & 1 \end{pmatrix} = 2 $$

Nota. Si el rango coincide con el número de vectores, entonces son linealmente independientes.

A continuación, verificaré si el punto P pertenece al plano.

Cómo determinar si un punto pertenece a un plano

Si el punto P pertenece al plano, deben existir dos parámetros t₁ y t₂ que satisfagan la siguiente combinación lineal, así como el sistema lineal correspondiente.

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 v_1 + t_2 v_2 $$

Sustituyo ahora los vectores directores:

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

A modo de referencia, elijo un punto P₀ perteneciente al plano. Por ejemplo, el extremo de uno de los vectores:

$$ \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} $$

Así, la expresión queda:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Ahora sustituyo las coordenadas (x, y, z) por las del punto (10,5,5) y compruebo si el sistema es compatible.

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

El sistema es compatible.

Para obtener el punto (10,5,5), basta con elegir t₁=1 y t₂=1.

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 + 3 + 4 \\ 1 + 1 + 3 \\ 2 + 2 + 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

Por tanto, la ecuación vectorial del plano es la siguiente:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Otra forma de comprobarlo. Para verificar la existencia de solución, también podría haber reformulado la ecuación vectorial como sigue: $$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 10-3 \\ 5-1 \\ 5-2 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 7 \\ 4 \\ 3 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ A continuación, se organizan los vectores de los coeficientes en una matriz columna: $$ \begin{pmatrix} 7 & 3 & 4 \\ 4 & 1 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ Si el rango de la matriz es inferior al número de vectores (es decir, menor que tres), entonces los vectores son linealmente dependientes y el sistema admite solución. En este caso, el rango de la matriz es dos (r_k=2), por lo que el sistema tiene solución. $$ r_k = 2 < 3 $$ La interpretación es sencilla: los vectores v₁(3,1,2) y v₂(4,3,1) son linealmente independientes, y para que el vector (7,4,3) pertenezca al plano, debe ser combinación lineal de v₁ y v₂.

Una vez obtenida la ecuación vectorial, resulta sencillo obtener la parametrización del plano.

Se trata simplemente de transformar la expresión en un sistema de ecuaciones:

$$ \begin{cases} x = 10 + t_1 \cdot 3 + t_2 \cdot 4 \\ y = 5 + t_1 \cdot 1 + t_2 \cdot 3 \\ z = 5 + t_1 \cdot 2 + t_2 \cdot 1 \end{cases} $$

$$ \begin{cases} x = 10 + 3t_1 + 4t_2 \\ y = 5 + t_1 + 3t_2 \\ z = 5 + 2t_1 + t_2 \end{cases} $$

Por último, para obtener la ecuación cartesiana del plano, se transforma la ecuación vectorial en tres segmentos:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x - 10 \\ y - 5 \\ z - 5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

A continuación, se organizan los tres vectores en una matriz columna:

$$ \begin{pmatrix} x - 10 & 3 & 4 \\ y - 5 & 1 & 3 \\ z - 5 & 2 & 1 \end{pmatrix} $$

El determinante de la matriz proporciona la ecuación cartesiana del plano.

De este modo, he obtenido también la ecuación cartesiana del plano.

Representación gráfica del plano en un sistema tridimensional:

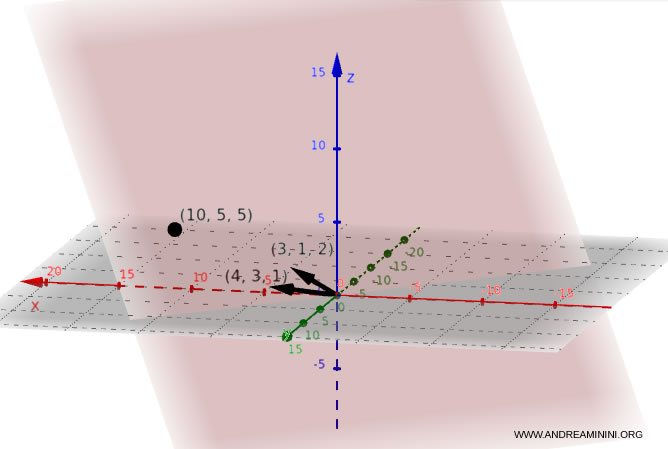
Conversión de la ecuación cartesiana a la ecuación paramétrica de un plano

Veamos ahora el proceso inverso. Partimos de la ecuación cartesiana de un plano y queremos obtener su ecuación paramétrica.

La ecuación cartesiana del plano es:

$$ ax + by + cz + d = 0 $$

La ecuación vectorial-paramétrica correspondiente es:

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

Los coeficientes a, b y c de la ecuación cartesiana definen el vector normal del plano, es decir, un vector perpendicular a dicho plano.

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

Si el vector normal es perpendicular al plano, también lo es a cualquier vector contenido en el mismo.

Por tanto, el vector normal es ortogonal a los vectores directores que intervienen en la ecuación paramétrica del plano.

Esto implica que el producto escalar entre el vector normal y cada vector director debe ser cero:

$$ \langle n , v_2 \rangle = 0 $$

$$ \langle n , v_1 \rangle = 0 $$

Esta condición nos permite determinar dos vectores linealmente independientes y ortogonales al vector normal, a partir de los cuales construiremos la ecuación vectorial/paramétrica del plano.

Ejemplo

Consideremos la siguiente ecuación cartesiana:

$$ -5x -y +8z + 15 = 0 $$

El vector normal correspondiente es:

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

Este vector normal es ortogonal al plano definido por la ecuación cartesiana.

Por tanto, también es ortogonal a cualquier vector no nulo contenido en el plano.

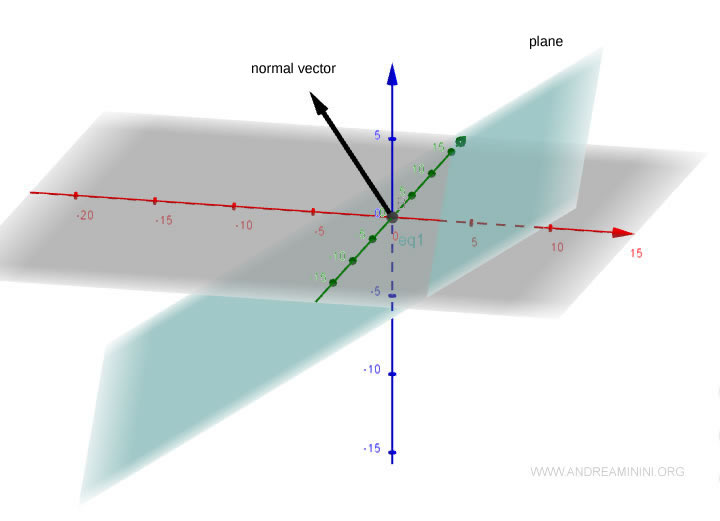
A continuación, debemos encontrar dos vectores linealmente independientes y ortogonales al vector normal.

Para ello, anulamos una de las componentes del vector normal, invertimos las otras dos y cambiamos el signo de una de estas últimas.

Por ejemplo, anulamos la componente x del vector normal:

$$ \begin{pmatrix} 0 \\ -1 \\ 8 \end{pmatrix} $$

Invertimos las otras dos componentes:

$$ \begin{pmatrix} 0 \\ 8 \\ -1 \end{pmatrix} $$

Y cambiamos el signo de una de ellas:

Así obtenemos el primer vector director del plano:

$$ v_1 = \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} $$

Aplicando el mismo método, hallamos el segundo vector director:

Anulamos ahora la componente y:

$$ \begin{pmatrix} -5 \\ 0 \\ 8 \end{pmatrix} $$

Invertimos las otras dos componentes:

$$ \begin{pmatrix} 8 \\ 0 \\ -5 \end{pmatrix} $$

Y cambiamos el signo de una de ellas:

$$ v_2 = \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

De este modo, hemos obtenido dos vectores ortogonales al vector normal.

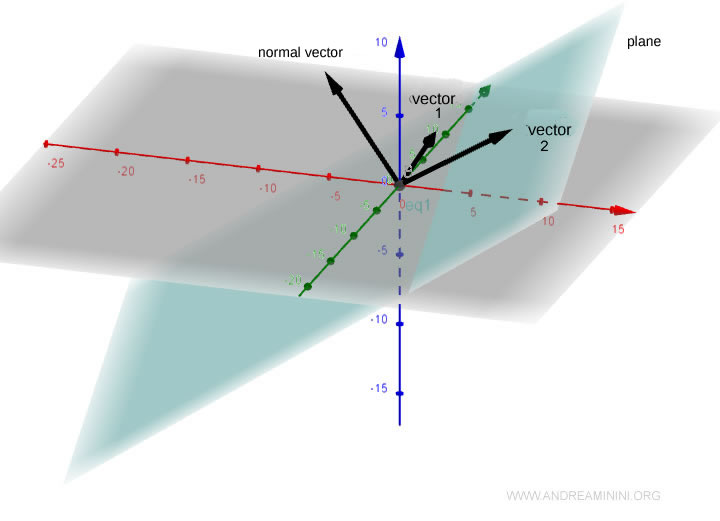
Comprobamos ahora que son vectores linealmente independientes:

$$ r_k \begin{pmatrix} 0 & 8 \\ 8 & 0 \\ 1 & 5 \end{pmatrix} = 2 $$

El rango de la matriz que contiene los vectores como columnas es igual a 2, es decir, al número de vectores.

Por tanto, los dos vectores son linealmente independientes.

A continuación, verificamos que también son ortogonales al vector normal:

$$ \langle n , v_1 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} \rangle = 0 $$

$$ \langle n , v_2 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} \rangle = 0 $$

El producto escalar es cero.

Por tanto, los vectores v₁ y v₂ son ortogonales al vector normal.

Podemos utilizarlos como vectores directores del plano.

Una vez comprobada su independencia lineal y su ortogonalidad, sustituimos v₁ y v₂ en la ecuación vectorial del plano:

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

Esta es la ecuación paramétrica del plano y de todos los planos paralelos.

Para restringir la ecuación al plano concreto que nos interesa, basta con añadir un punto P₀ perteneciente al plano.

Por ejemplo, asignamos x = 0 y z = 0 en la ecuación cartesiana para determinar la coordenada y:

$$ -5x -y +8z + 15 = 0 \\ -5(0) -y +8(0) + 15 = 0 \\ y = 15 $$

Así obtenemos un punto arbitrario del plano: P(x, y, z) = (0, 15, 0).

Sustituyendo este punto en la ecuación vectorial, obtenemos la ecuación vectorial del plano:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 15 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

A partir de la ecuación vectorial, es sencillo obtener la ecuación paramétrica del plano:

Simplemente transformamos los vectores en un sistema de ecuaciones:

$$ \begin{cases} x = 8t_2 \\ y = 15 + 8t_1 \\ z = t_1 + 5t_2 \end{cases} $$

Obtención de la ecuación cartesiana a partir del vector normal

Consideremos la siguiente ecuación cartesiana:

$$ -5x -y +8z + 15 = 0 $$

El vector normal correspondiente es:

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

El vector normal es ortogonal al plano cartesiano.

Seleccionemos un punto arbitrario del plano.

Para determinar la coordenada x, fijamos y = 0 y z = 0:

$$ -5x -y +8z + 15 = 0 $$

$$ -5x - (0) + 8(0) + 15 = 0 $$

$$ x = 15 $$

Así obtenemos un punto del plano:

$$ P_1 = \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} $$

Consideremos ahora un punto genérico del plano:

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

Calculamos el vector que une ambos puntos:

$$ P_1P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} x - 15 \\ y \\ z \end{pmatrix} $$

Este vector es un vector genérico contenido en el plano.

Sabemos que cualquier vector contenido en el plano debe ser ortogonal al vector normal.

Por tanto, el producto escalar <v, n> debe ser cero:

$$ < P_1P , n > = 0 $$

Realizamos el cálculo del producto escalar:

$$ \left\langle \begin{pmatrix} x - 15 \\ y \\ z \end{pmatrix} , \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} \right\rangle = -5(x - 15) - y + 8z = 0 $$

$$ -5x + 75 - y + 8z = 0 $$

De este modo, obtenemos nuevamente la ecuación cartesiana del plano.

Y así sucesivamente.