Rango de una matriz

El rango de una matriz A es el orden más alto de un menor que no se anula. También se lo conoce como la característica de la matriz.

Dada una matriz A de dimensiones mxn, su rango es p si existe al menos un menor de orden p con determinante distinto de cero, y todos los menores de orden p+1, si existen, tienen determinante nulo.

El rango de una matriz A es un número real que se puede denotar como rk(A), rg(A), r(A) o p(A).

Nota. En pocas palabras, el rango de una matriz es el mayor orden de los menores cuyo determinante no es cero.

¿Para qué sirve el rango?

El rango indica cuántas filas o columnas de una matriz son linealmente independientes.

Cómo se calcula el rango de una matriz

Si la matriz A pertenece a M_mxn, entonces su rango, denotado como r(A), está comprendido entre cero y el menor de los dos valores m y n.

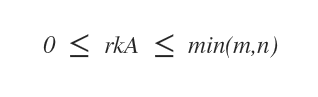
El rango representa el número máximo de filas o columnas linealmente independientes dentro de la matriz.

Por lo tanto, dicho número no puede superar ni el total de filas ni el de columnas.

Nota. Por convención, solo la matriz nula tiene rango cero. Todas las demás matrices tienen rango mayor o igual que uno.

Un ejemplo práctico

Veamos ahora cómo calcular el rango de una matriz de 3x4.

En este caso, el rango de la matriz es 3.

Nota. Al calcular el rango, no es necesario examinar todos los menores de todos los órdenes. Basta con identificar un menor no nulo de orden N y luego analizar los de orden N+1.

Rango máximo o completo

Una matriz tiene rango completo o rango máximo cuando su rango es igual a min(m,n).

Ejemplo práctico

A continuación, un ejemplo de matriz con rango completo.

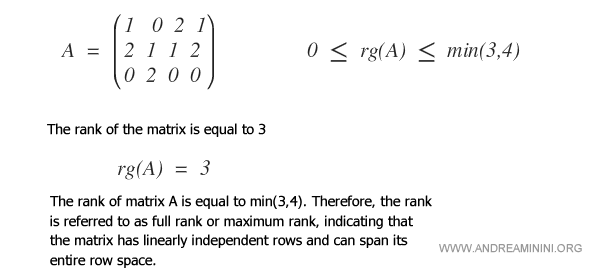
Nota. En matrices cuadradas de orden n, el rango solo puede ser igual a n - es decir, rg(A)=n - si el determinante de la matriz es distinto de cero.

Propiedades del rango

El rango de una matriz cumple con las siguientes propiedades fundamentales:

1. El rango de una matriz A es igual al rango de su transpuesta A^T.
   
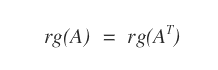
2. El rango es igual a cero solo cuando la matriz es completamente nula.
3. Si todos los menores de orden N son nulos, entonces también lo serán todos los menores de orden superior.

   Demostración. Supongamos que todos los menores de orden k de una matriz son nulos, con k menor que el mínimo entre m y n (k<min{m,n}). Consideremos un menor de orden j con k<j≤min{m,n}. Mediante la expansión de Laplace, el determinante de orden j se expresa en función de determinantes de submatrices cuadradas de orden j−1. Este proceso continúa hasta alcanzar determinantes de orden k. Como los menores de orden k son nulos, todos los menores de orden superior también deben serlo.

Otros métodos para determinar el rango

Existen diversas técnicas para calcular el rango de una matriz.

Un método directo consiste en calcular todos los menores, aunque puede resultar poco eficiente.

Para agilizar el proceso, se pueden aplicar métodos alternativos como el teorema de Kronecker o la eliminación de Gauss.

Rango y representación vectorial en álgebra lineal

El rango de una matriz - formada por vectores fila o columna - indica cuánta información independiente contiene en términos espaciales.

Por ejemplo, consideremos la matriz 2x3:

$$ M_1 = \begin{pmatrix} 1 & 0 & 3 \\ 0 & 2 & 1 \end{pmatrix} $$

Esta matriz tiene rango 2.

$$ rk(M_1)= 2 $$

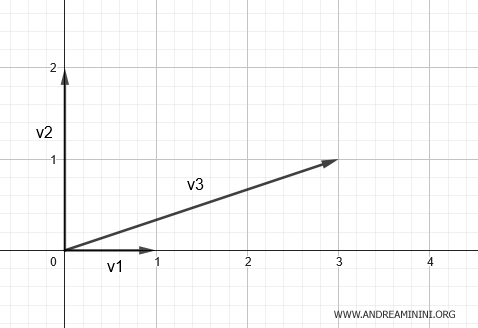
Esto significa que los vectores columna v1=(1;0), v2=(0;2) y v3=(3;1) pueden representarse en dos direcciones independientes, es decir, generan un plano.

Veamos otro ejemplo para mayor claridad:

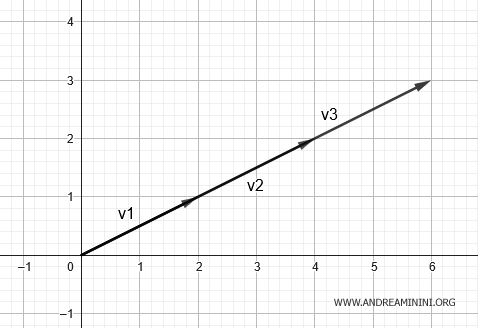
$$ M_2 = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \end{pmatrix} $$

Esta matriz tiene rango 1, ya que una fila es múltiplo escalar de la otra; por tanto, hay redundancia.

$$ rk(M_2)= 1 $$

Esto implica que los vectores v1=(2;1), v2=(4;2) y v3=(6;3) están contenidos en un mismo subespacio unidimensional, es decir, sobre una recta.

En estos casos, falta una dimensión en la representación vectorial.

Nota sobre dimensiones superiores. En matrices de dimensión mayor a 3, aunque la representación gráfica no sea viable, el rango sigue siendo una medida clave para cuantificar la independencia entre vectores.

Observaciones

Algunas observaciones útiles sobre el rango de una matriz:

• Dos matrices A y B son equivalentes por filas si y solo si tienen el mismo rango: $$ rk(A) = rk(B) $$ Esto aplica tanto a matrices cuadradas como rectangulares.
• El rango es invariante respecto a la transposición: el rango de una matriz M es igual al de su transpuesta M^T, es decir: $$ rk(M) = rk(M^T) $$