Matrices

Introducción a las matrices

Una matriz es una tabla ordenada de elementos a_i,j, donde cada a_i,j representa un número llamado elemento (o coeficiente), y los subíndices i y j indican, respectivamente, el número de fila y de columna del elemento.

Si los elementos de la matriz A son números reales, se le denomina matriz de coeficientes reales.

$A : = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1j} & ... & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2j} & ... & a_{2n} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \dots & a_{ij} & \dots & a_{in} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mj} & \dots & a_{mn} \end{pmatrix}$

Un elemento genérico (i,j) se ubica en la i-ésima fila y en la j-ésima columna.

ejemplo

Los índices de los elementos pueden escribirse con o sin coma (a_m,n o a_mn).

Nota. La notación con coma evita confusiones cuando los índices son mayores a diez.

Otras notaciones que se utilizan para representar matrices incluyen A_(m,n) , A_mxn o A=(a_mn).

otras notaciones

El número total de filas y columnas (m x n) se conoce como la dimensión de la matriz.

dimensión de matriz

Así, m y n representan las dimensiones de una matriz de tipo (m, n).

Si el número de filas coincide con el de columnas (m = n), se llama matriz cuadrada.

¿Para qué sirve una matriz? Las matrices son herramientas matemáticas usadas principalmente en álgebra lineal para representar y resolver sistemas de m ecuaciones y n incógnitas.

Ejemplo de una matriz
Conjuntos de matrices
Tipos de matrices
Cómo representar un sistema lineal con una matriz

Ejemplo de una matriz

A continuación, se muestra un ejemplo de matriz de tipo (2,3).

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

Los elementos de la matriz son:$$ a_{11}=3 \\ a_{12} = 1 \\ a_{13} = 6 \\ a_{21}=0 \\ a_{22} = 4 \\ a_{23} = -1 $$

Donde los elementos a₁₁, a₁₂ y a₁₃ son los coeficientes de la primera fila de la matriz.

Los elementos a₂₁, a₂₂ y a₂₃ son los coeficientes de la segunda fila de la matriz.

Nota. En una matriz en álgebra lineal, el orden de los elementos es fundamental. Cambiar el orden genera una matriz distinta. Por ejemplo, si definimos una matriz B invirtiendo las filas de la matriz A: $$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$ $$ B : = \begin{pmatrix} 0 & 4 & -1 \\ 3 & 1 & 6 \end{pmatrix} $$ entonces A y B tendrían los mismos elementos, pero serían matrices diferentes. Es importante tener esto en cuenta.

Conjuntos de matrices

El conjunto de todas las matrices mxn con elementos reales (matrices reales) se representa con la notación M_m,n(R) o M(m,n,R).

$$ M_{m,n}(R) = M(m,n,R) $$

El conjunto de matrices cuadradas se indica así:

$$ M_{n,n}(R) = M(n,n,R) $$

Ejemplo

La matriz A tiene 2 filas y 3 columnas.

$$ A : = \begin{pmatrix} 3 & 1 & 6 \\ 0 & 4 & -1 \end{pmatrix} $$

Por lo tanto, la matriz A pertenece al conjunto de matrices de dimensión 2x3.

$$ A \in M(2,3,R) $$

Nota. La matriz A pertenece al conjunto de matrices 2x3 con coeficientes reales, representado por M(2,3,R). Así, sus elementos no solo pueden ser enteros, sino también reales (R). Si se requiere una matriz únicamente de enteros, se escribiría M(2,3,Z) donde Z representa el conjunto de los números enteros. El conjunto M(2,3,Z) es un subconjunto de M(2,3,R) ya que, para matrices de igual dimensión, los enteros son un subconjunto de los reales, es decir, Z⊂R.

Tipos de matrices

Según sus dimensiones, número de filas y columnas, se pueden clasificar los siguientes tipos de matrices:

Matrices rectangulares. Son matrices con más de una fila (m>1) y al menos una columna (n>0), en las que el número de filas no coincide con el número de columnas (m≠n). Esta característica es la que les da su forma rectangular.
Matriz cuadrada. Una matriz cuadrada tiene igual número de filas y columnas (m=n), adquiriendo así una forma cuadrada.
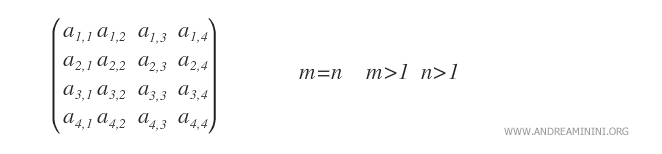
Matriz fila. Una matriz fila es una matriz de 1xn con solo una fila (m=1).
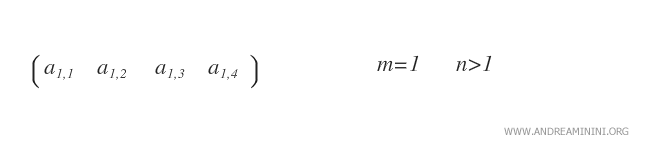
Matriz columna. Una matriz columna es una matriz mx1 con solo una columna (n=1).
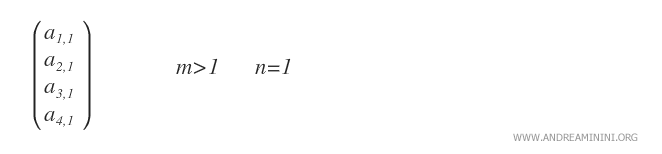
Matriz nula. Una matriz nula carece de elementos, y por ende, de filas (m=0) y de columnas (n=0).

Cómo representar un sistema lineal con una matriz

Dado un sistema lineal A compuesto por m ecuaciones y n incógnitas

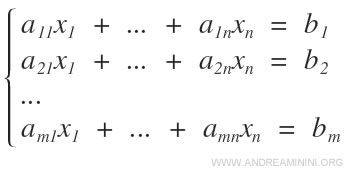
ejemplo de sistema lineal

este sistema puede asociarse siempre a dos matrices:

La matriz de coeficientes (o matriz incompleta) es una matriz de m por n, donde cada elemento es el coeficiente amn de las ecuaciones del sistema.
La matriz aumentada (o matriz completa) es una matriz de m filas y n+1 columnas, compuesta tanto por los coeficientes a_mn como por las constantes b_m del sistema lineal. Esta matriz combina la matriz de coeficientes A con el vector columna de constantes B, también conocida como matriz aumentada o bordeada del sistema AX.

Nota. Básicamente, la matriz aumentada es la matriz de coeficientes a la que se le añade la columna de términos constantes cuando trabajamos con matrices y ecuaciones en álgebra lineal.

Ejemplo práctico de matrices y ecuaciones en álgebra lineal

Este sistema lineal consta de dos ecuaciones y tres incógnitas. La matriz de coeficientes A es la siguiente:

ejemplo de sistema lineal

La matriz de coeficientes A es la siguiente:

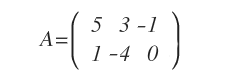
la matriz de coeficientes

Nota. En la segunda ecuación del sistema (x₁-4x₂=6), la variable x₃ no aparece. En tales casos, el elemento correspondiente de la matriz se asigna con un valor de cero.

La matriz completa A|B del sistema es la siguiente:

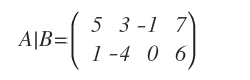
la matriz aumentada

Nota. Simplemente se añade la columna de constantes a la matriz de coeficientes.

Y así sucesivamente