Matriz diagonal
Una matriz cuadrada se denomina matriz diagonal cuando todos los elementos situados fuera de la diagonal principal son iguales a cero.

Es decir, si \( i \neq j \), entonces \( a_{ij} = 0 \).
Ejemplo
Consideremos, por ejemplo, una matriz diagonal de orden 3, es decir, con tres filas y tres columnas.
Como puede apreciarse, todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
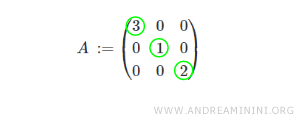
Nota: Los elementos de la diagonal principal pueden ser cero o distintos de cero.
Por tanto, una matriz diagonal se considera un caso particular tanto de matriz triangular superior como de matriz triangular inferior.

En el ámbito matemático, el conjunto de matrices diagonales de orden \( n \) con coeficientes reales se denota por \( D(n, R) \), donde \( n \) representa el orden de la matriz y \( R \) el conjunto de los números reales.
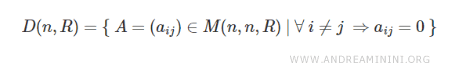
En resumen, las matrices diagonales desempeñan un papel fundamental en el álgebra lineal y tienen aplicaciones esenciales en diversas ramas de las matemáticas y de las ciencias aplicadas.