Matrices (Preguntas Frecuentes)

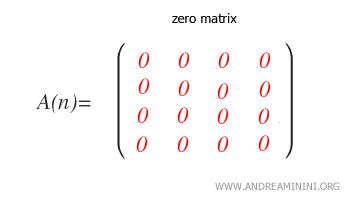
1. ¿Qué es una matriz nula?
   Es una matriz en la que todos sus elementos son iguales a cero.
   
2. ¿Qué es una matriz cuadrada?
   Es una matriz que tiene el mismo número de filas y columnas (m = n).
   
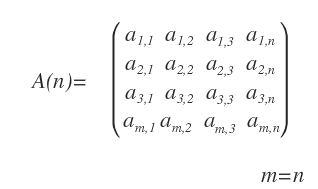
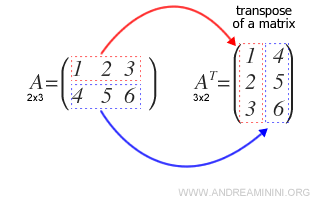
3. ¿Qué es la matriz transpuesta?
   La transpuesta de una matriz A^T se obtiene intercambiando sus filas por columnas.
   
4. ¿Qué es la matriz opuesta?
   Es la matriz -A, cuyos elementos tienen el mismo valor absoluto que los de una matriz A, pero con signo contrario.
   
5. ¿Qué son matrices equivalentes?
   Dos matrices se consideran equivalentes si representan sistemas lineales con el mismo conjunto de soluciones.
   
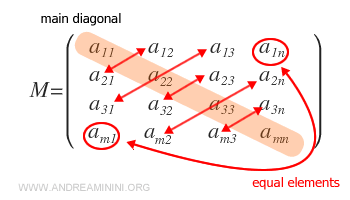
6. ¿Qué es una matriz simétrica?
   Es una matriz cuadrada cuyos elementos son simétricos respecto a la diagonal principal, es decir, a_ij = a_ji.
   
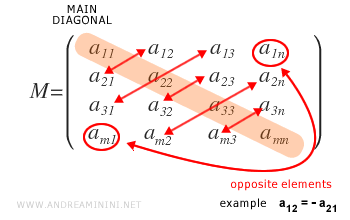
7. ¿Qué es una matriz antisimétrica?
   Es una matriz cuadrada en la que a_ij = - a_ji para todos sus elementos simétricos respecto a la diagonal principal.
   
8. ¿Qué es una matriz diagonal?
   Es una matriz cuadrada cuyos elementos fuera de la diagonal principal son todos cero. Solo los elementos de la diagonal pueden ser distintos de cero.
   
9. ¿Qué es la matriz identidad?
   Es una matriz diagonal cuyos elementos en la diagonal principal son todos iguales a uno. Es un caso particular de matriz escalar.
   
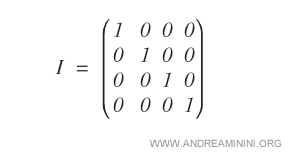
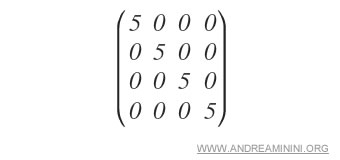
10. ¿Qué es una matriz escalar?
    Es una matriz cuadrada en la que todos los elementos de la diagonal principal son iguales entre sí y distintos de cero.
    
11. ¿Qué es una matriz invertible?
    Una matriz cuadrada A de orden n es invertible si existe otra matriz A ^{- 1} del mismo orden tal que A·A ^{- 1} = A ^{- 1}·A = I_n.
    
12. ¿Qué es una matriz ortogonal?
    Es una matriz cuadrada e invertible cuya transpuesta es igual a su inversa: A^T = A ^{- 1}.
    
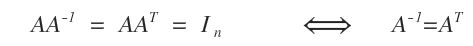
13. ¿Qué es el determinante?
    Es un número asociado a una matriz cuadrada que resume propiedades fundamentales de la misma. Se denota como det(A) o |A|.
    
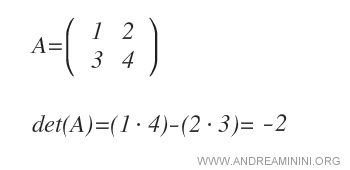
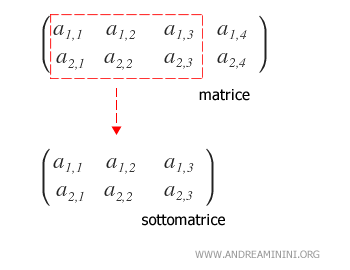
14. ¿Qué es una submatriz?
    Es una matriz que se obtiene al eliminar una o más filas y/o columnas de otra matriz.
    
15. ¿Qué es una submatriz complementaria?
    Es una submatriz de orden inferior que se obtiene al eliminar una única fila y una única columna de la matriz original.
    
16. ¿Qué es un menor de una matriz?
    Es el determinante de una submatriz cuadrada que se obtiene eliminando i filas y j columnas de la matriz original.
    
17. ¿Qué es el menor complementario?
    Es el determinante de una submatriz que se obtiene eliminando la fila i-ésima y la columna j-ésima de una matriz cuadrada A.
    
18. ¿Qué es el cofactor?
    El cofactor (o complemento algebraico) de un elemento a_ij es su menor complementario multiplicado por ( - 1)^i+j.
    
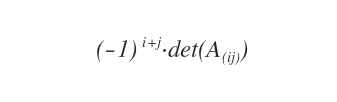
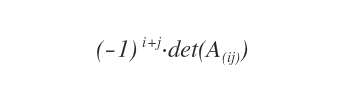
19. ¿Qué es la matriz adjunta?
    Es la transpuesta de la matriz de cofactores.
    
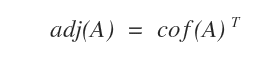
20. ¿Qué es la traza de una matriz?
    Es la suma algebraica de los elementos situados sobre la diagonal principal.
    
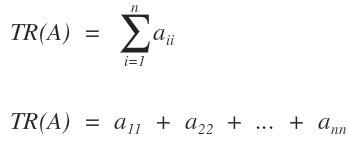
21. ¿Qué es el rango de una matriz?
    Es el mayor orden entre todos los menores no nulos que pueden extraerse de la matriz.
22. ¿Qué es una matriz singular?
    Es una matriz cuadrada cuyo determinante es igual a cero; por tanto, no es invertible.
23. ¿Qué son matrices semejantes?
    Dos matrices A y B son semejantes si existe una matriz invertible M tal que se cumple: M ^{- 1}AM = B.