Determinante de una matriz

En álgebra lineal, el determinante de una matriz cuadrada es un valor escalar que proporciona información esencial sobre sus propiedades. Se representa como det(A) o |A|, y resume tanto aspectos algebraicos como geométricos de la matriz.

Ejemplo

Consideremos la siguiente matriz cuadrada:

$$ A= \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

Su determinante se expresa como det(A):

$$ det(A) = -2 $$

O bien, utilizando la notación con barras verticales:

$$ | A | = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$

Nota. El determinante solo está definido para matrices cuadradas, es decir, aquellas con el mismo número de filas y columnas (m = n).

Cálculo del determinante de una matriz

Matrices cuadradas de orden 1

En una matriz de 1x1, que contiene un único elemento, el determinante coincide simplemente con el valor de dicho elemento, a₁₁.

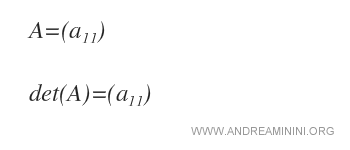
Ejemplo. La matriz A es de orden 1 y contiene un solo elemento: a₁₁ = 5. Por tanto, det(A) = 5.

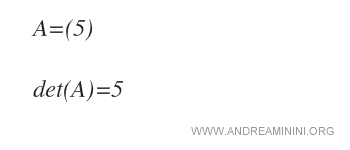
Matrices cuadradas de orden 2

Para una matriz de 2x2, el determinante se obtiene multiplicando los elementos de la diagonal principal (a₁₁·a₂₂) y restando el producto de los elementos de la diagonal secundaria (a₂₁·a₁₂).

Ejemplo. Para la siguiente matriz A de orden 2, compuesta por dos filas y dos columnas, se tiene det(A) = -2.

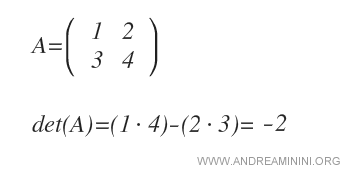
Regla de Sarrus

La regla de Sarrus es un método específico para calcular el determinante de matrices cuadradas de orden 3 (es decir, 3x3).

Consideremos una matriz de 3x3:

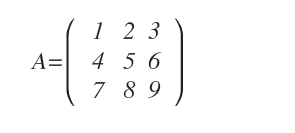
Repetimos las dos primeras columnas a la derecha:

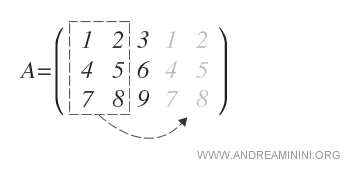
A continuación, sumamos los productos de las diagonales que van desde la esquina superior izquierda hasta la inferior derecha:

Después restamos los productos de las diagonales que van desde la esquina inferior izquierda hasta la superior derecha:

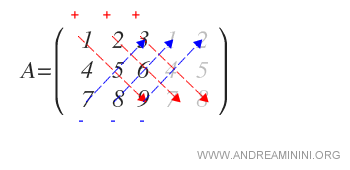
La suma algebraica de estos productos nos da el valor del determinante.

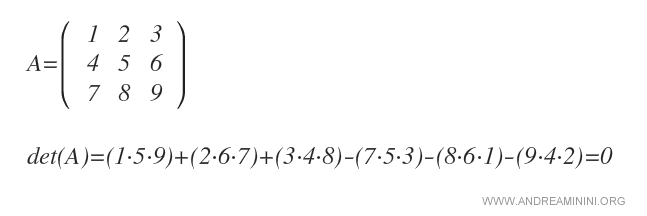
Resumen de la regla de Sarrus

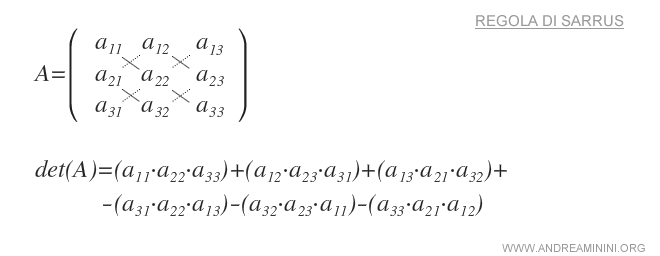
Método de Laplace

El método de Laplace es una de las técnicas más utilizadas para calcular determinantes, ya que permite descomponer un determinante de orden n en una combinación de determinantes menores de orden n−1.

Debe su nombre al matemático Pierre-Simon Laplace y se basa en el desarrollo por cofactores.

¿Cómo funciona?

El método consiste en expresar el determinante como una suma alternada de productos entre elementos de una fila o columna y los determinantes de sus menores complementarios.

1. Selecciona cualquier columna j de la matriz.

   ¿Cuál conviene elegir? Aunque cualquier columna es válida, suele ser preferible escoger aquella con mayor número de ceros para simplificar los cálculos.

2. Una vez elegida la columna j, se eliminan la fila i y la columna j asociadas a cada elemento, y se calculan los determinantes de las submatrices resultantes utilizando la fórmula de Laplace.
   

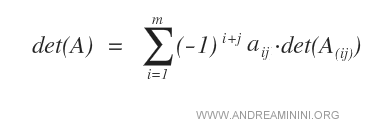
Ejemplo. Para calcular el determinante de una matriz A de orden 3, aplicamos el desarrollo por cofactores sobre la columna j = 1. Al sumar los determinantes de los menores correspondientes, obtenemos: det(A) = 0.

Desarrollo por filas

El desarrollo de Laplace también puede aplicarse seleccionando una fila en lugar de una columna.

En ese caso, la fórmula se adapta recorriendo todas las columnas j de la fila seleccionada.

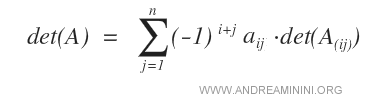
Este procedimiento conduce al mismo resultado final.

Ejemplo. En este caso, desarrollamos por la primera fila: $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 0 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 0 & 1 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 1 \cdot \begin{vmatrix} 0 & 1 & 2 \\ 0 & 0 & 5 \\ 0 & 0 & 0 \end{vmatrix} $$ Evaluamos los menores: $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 10 - 3 \cdot 0 + 5 \cdot 0 - 1 \cdot 0 = 20 $$

Consejo para simplificar los cálculos. Para agilizar el proceso, conviene escoger la fila o columna con más ceros. En este ejemplo, seleccionamos la cuarta fila: $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = -0 \cdot A_{(4,1)} + 0 \cdot A_{(4,2)} - 0 \cdot A_{(4,3)} + 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Gracias a los ceros, evitamos calcular tres menores. Repetimos el procedimiento con la tercera fila de la submatriz: $$ = 2 \cdot 5 \cdot \begin{vmatrix} 2 & 3 \\ 0 & 1 \end{vmatrix} = 2 \cdot 5 \cdot (2 \cdot 1) = 20 $$ En este caso, como la matriz es triangular, también podríamos haber obtenido el determinante multiplicando los elementos de su diagonal principal: $$ 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Limitaciones del método de Laplace. Aunque es útil para matrices pequeñas, este método resulta ineficiente para órdenes elevados. En esos casos, es preferible recurrir a técnicas como la eliminación de Gauss.

Método de eliminación de Gauss

El método de eliminación de Gauss es una técnica eficaz que también permite calcular el determinante de una matriz cuadrada.

Mediante transformaciones elementales por filas, se transforma la matriz en una forma triangular superior.

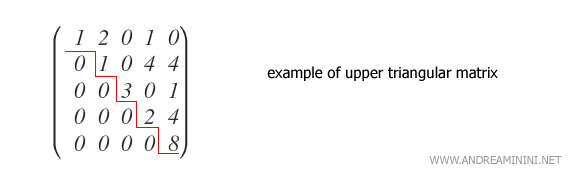
En una matriz triangular, el determinante se obtiene multiplicando los elementos de la diagonal principal, lo cual simplifica notablemente el cálculo.

No obstante, es fundamental tener en cuenta los efectos de las operaciones elementales sobre el signo y el valor del determinante:

• Intercambiar dos filas (Rx ⇔ Ry) cambia el signo del determinante (multiplicación por −1).
• Multiplicar una fila por un escalar k modifica el determinante multiplicándolo por k.
• Sumar a una fila un múltiplo de otra (Rx + k·Ry) no altera el valor del determinante.

Ejemplo. En el siguiente ejercicio, aplicamos la eliminación de Gauss para calcular el determinante de la matriz A:

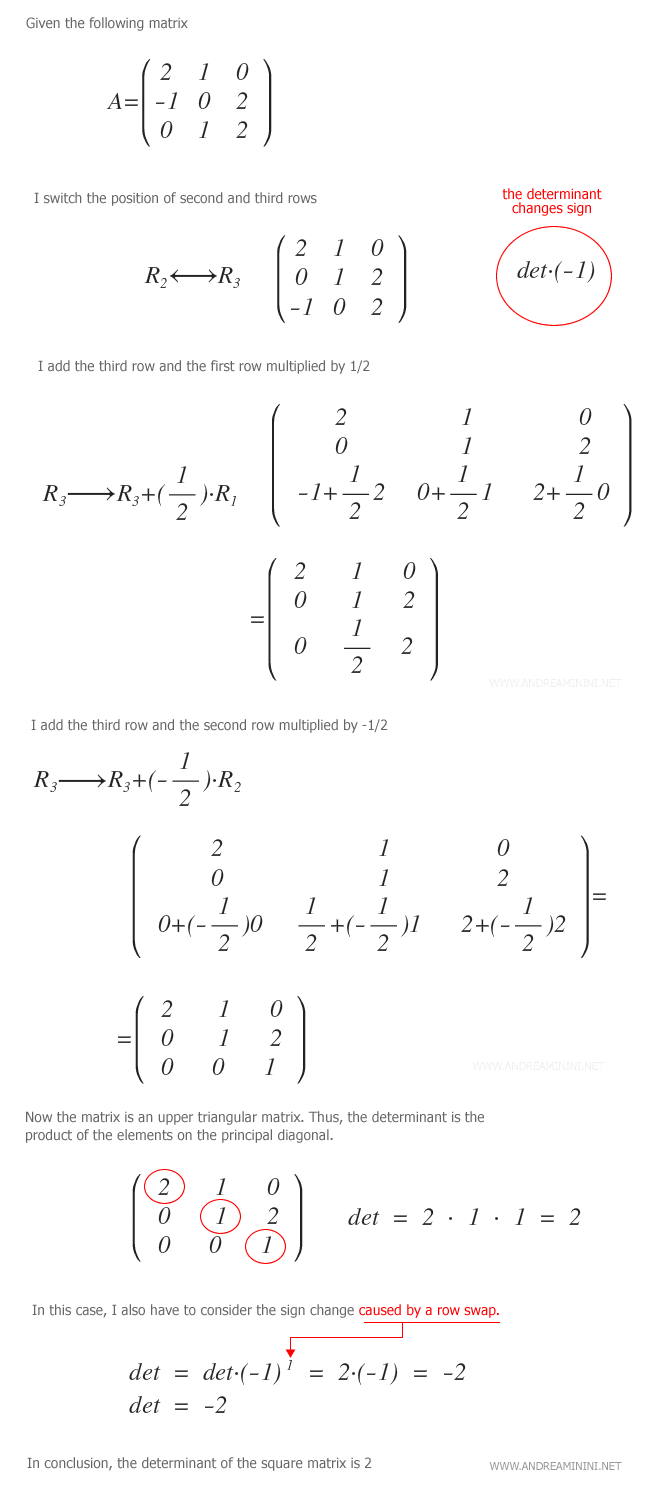
Ventajas del método de Gauss

Cuando se trabaja con matrices de gran dimensión, la eliminación de Gauss resulta mucho más eficiente que el desarrollo por cofactores de Laplace.

Propiedades del determinante

A continuación se presentan algunas propiedades fundamentales del determinante de matrices cuadradas:

• Si una fila o una columna está compuesta exclusivamente por ceros, el determinante es igual a cero.

  Ejemplo:
  $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 7 & 8 & 9 \end{vmatrix} = 0 \quad \begin{vmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 0 \end{vmatrix} = 0 $$

• Si la matriz es diagonal, triangular superior o triangular inferior, el determinante es igual al producto de los elementos de su diagonal principal.

  Ejemplo:
  $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{vmatrix} = 1 \cdot 5 \cdot 9 = 45 $$

• El determinante de una matriz es igual al de su traspuesta: $$ \det(A) = \det(A^T) $$

  Ejemplo:
  $$ \det\left(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\right) = -2 \quad \det\left(\begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}\right) = -2 $$

• Si una matriz tiene dos filas o dos columnas idénticas, su determinante es cero.

  Ejemplo:
  $$ \det\left(\begin{pmatrix} a & b \\ a & b \end{pmatrix}\right) = ab - ba = 0 $$
  $$ \det\left(\begin{pmatrix} a & b & c \\ a & b & c \\ d & e & f \end{pmatrix}\right) = 0 $$
  Lo mismo ocurre si hay dos columnas iguales, ya que la traspuesta tendrá dos filas iguales.

• El intercambio de dos filas (o columnas) invierte el signo del determinante.

  Ejemplo:
  $$ \det\left(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\right) = -2 $$
  $$ \det\left(\begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix}\right) = 2 $$

• Teorema de Binet: si \( A \) y \( B \) son matrices cuadradas del mismo orden, entonces: $$ \det(A \cdot B) = \det(A) \cdot \det(B) $$

  Ejemplo:
  $$ A = \begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix},\quad B = \begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} $$
  $$ \det(A) = -10,\quad \det(B) = 1 $$
  $$ A \cdot B = \begin{pmatrix} 22 & 13 \\ 16 & 9 \end{pmatrix},\quad \det(A \cdot B) = -10 $$
  $$ \det(A) \cdot \det(B) = -10 $$

• Para cualquier matriz cuadrada \( M \) de orden \( n \) y un escalar \( k \), se cumple: $$ \det(k \cdot M) = k^n \cdot \det(M) $$

  Demostración:
  $$ k \cdot M = \begin{pmatrix} ka & kb \\ kc & kd \end{pmatrix},\quad \det(k \cdot M) = k^2 \cdot \det(M) $$
  Ejemplo: $$ M = \begin{pmatrix} 6 & 8 \\ 4 & 2 \end{pmatrix} = 2^2 \cdot \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix} $$
  $$ \det(M) = 4 \cdot (3 \cdot 1 - 4 \cdot 2) = -20 $$

• Si una fila o columna es múltiplo exacto de otra, el determinante es nulo.

  Ejemplo:
  $$ \det\left(\begin{pmatrix} 2 & 4 \\ 4 & 8 \end{pmatrix}\right) = 0 $$

Determinante de matrices triangulares

El determinante de una matriz triangular se calcula como el producto de los elementos que componen su diagonal principal.

Esto ocurre porque todos los demás términos en el desarrollo del determinante se anulan.

En consecuencia, el cálculo del determinante de una matriz triangular es inmediato y no requiere operaciones complejas.

Ejemplo

Consideremos la siguiente matriz:

$$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$

Como \( A \) es una matriz triangular, su determinante se obtiene multiplicando los elementos de su diagonal principal:

$$ \det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Observaciones fundamentales

A continuación, se destacan algunas propiedades esenciales del determinante:

• El determinante constituye un invariante completo bajo la operación de transposición. Es decir, una matriz cuadrada \( M \) y su traspuesta \( M^T \) comparten el mismo determinante: $$ \det(M) = \det(M^T) $$

Calculadora de determinantes en línea

Utiliza esta herramienta para calcular el determinante de cualquier matriz cuadrada de forma rápida y sencilla.

Y así sucesivamente