Matriz triangular

Una matriz cuadrada se denomina matriz triangular cuando todos sus elementos no nulos se encuentran exclusivamente por encima o por debajo de la diagonal principal.

Tipos de matrices triangulares

Las matrices triangulares se clasifican en dos categorías principales: superiores e inferiores.

• Triangular superior. Todos los elementos no nulos se sitúan por encima de la diagonal principal, la cual puede contener o no valores distintos de cero.
  
  

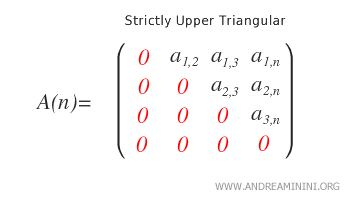
  Triangular superior estricta. Una matriz es estrictamente triangular superior si todos sus elementos no nulos están estrictamente por encima de la diagonal principal, mientras que esta y todos los elementos situados por debajo de ella son cero. Es decir, para cada entrada \( a_{ij} \), se cumple \( i < j \).
  

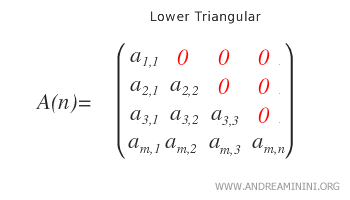
• Triangular inferior. Una matriz es triangular inferior si todos los elementos no nulos aparecen por debajo de la diagonal principal, que también puede contener elementos distintos de cero.
  
  

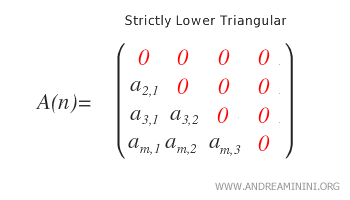
  Triangular inferior estricta. Una matriz es estrictamente triangular inferior si todos sus elementos no nulos se encuentran exclusivamente por debajo de la diagonal principal, la cual está compuesta únicamente por ceros. Es decir, se cumple \( i > j \) para todas las entradas distintas de cero.
  

Propiedades de las matrices triangulares

Entre las propiedades más destacadas de este tipo de matrices, cabe mencionar:

• Determinante
  El determinante de una matriz triangular, ya sea superior o inferior, es igual al producto de los elementos de su diagonal principal.

  Ejemplo: Consideremos la siguiente matriz triangular: $$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$ Como todos los términos fuera de la diagonal no afectan al cálculo, el determinante se obtiene multiplicando los elementos diagonales: $$ \det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Y así sucesivamente...