Teorema de la matriz ampliada
El teorema de la matriz ampliada es un método eficaz para determinar el rango de una matriz sin necesidad de calcular todos los menores de orden k.
También se le conoce como método de ampliación, teorema de Orlando o teorema de Kronecker.
Definición
Sea b un menor no nulo de orden k correspondiente a una submatriz B de la matriz A.
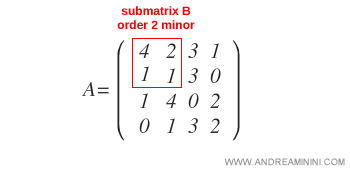
Nota. El menor es el determinante de la submatriz B: $$ \Delta_B = 4 \cdot 1 - 2 \cdot 1 = 2 $$
Si todos los menores de orden k+1 obtenidos al ampliar la submatriz B resultan ser nulos...
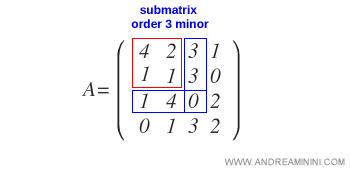
¿Qué significa ampliar una submatriz? Es similar a añadir un borde a una manta: se incorporan una fila y una columna adicionales a la submatriz original de orden k, seleccionadas entre las restantes de la matriz. Así se obtiene una submatriz de orden k+1. Los menores correspondientes reciben el nombre de ampliaciones de B.
Si todos los menores de orden k+1 son nulos, entonces el rango de la matriz A es exactamente k.
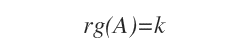
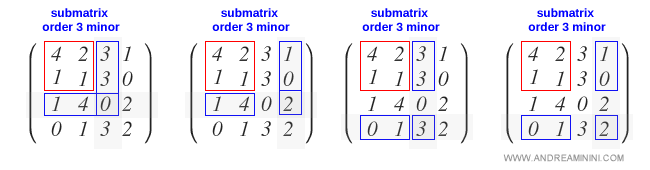
Nota. Es posible generar más de una submatriz ampliada. Por ejemplo, la submatriz B puede ampliarse de distintas formas combinando las filas y columnas restantes de la matriz A. En este caso, hay 4 combinaciones posibles, y por tanto, cuatro submatrices ampliadas cuyos menores deben evaluarse.
Ejemplo práctico
Consideremos la siguiente matriz de 4x4, cuyo rango puede estar entre 0 y 4.
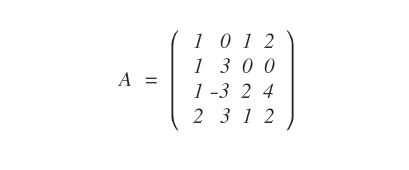
Como contiene al menos un elemento distinto de cero, el rango debe estar entre 1 y 4.
Para verificar si el rango es al menos 2, calculamos el determinante de una submatriz de orden 2x2.
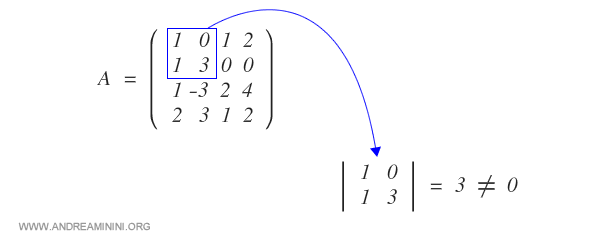
Dado que el menor de orden 2 es distinto de cero, el rango se encuentra entre 2 y 4.
A continuación, aplicamos el teorema de la matriz ampliada a dicha submatriz para investigar si el rango puede ser igual a 3.
La submatriz puede ampliarse de cuatro maneras distintas:
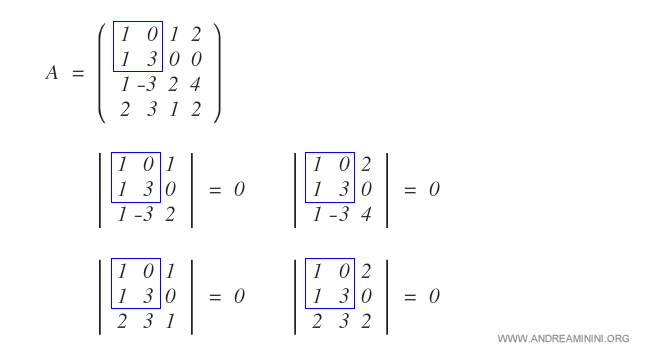
En todos los casos, los menores de las matrices ampliadas resultan ser nulos.
Según el teorema de la matriz ampliada, la matriz A no puede tener rango 3.
Y si no tiene rango 3, entonces tampoco puede alcanzar un rango superior (k > 3).
Por tanto, el rango máximo de esta matriz es k = 2, es decir: $$ rk(A) = 2 $$
Observaciones útiles
A continuación, algunas observaciones relevantes sobre el teorema de la matriz ampliada:
- Una matriz tiene rango $$ rk(M) = 0 $$ únicamente si es la matriz nula.
Demostración. Si M es la matriz nula (todos sus elementos son cero), entonces todos sus menores de orden 1 también lo serán.
- El rango de una matriz M es igual al de su transpuesta MT: $$ rk(M) = rk(M^T) $$
Explicación. Toda matriz cuadrada y su transpuesta tienen el mismo determinante. En consecuencia, el rango se conserva bajo transposición.
- Si una matriz M tiene rango $$ rk(M) = n $$, entonces todos sus menores de orden superior a n son necesariamente nulos.
- Si todos los menores de orden n son nulos, entonces el rango de la matriz es estrictamente menor que n: $$ rk(M) < n $$
Y así sucesivamente.