Determinación del rango mediante eliminación de Gauss
El rango de una matriz puede determinarse de forma eficiente mediante el procedimiento de eliminación de Gauss.
Sea A una matriz de dimensión m × n y sea B una forma escalonada por filas obtenida a partir de A mediante eliminación de Gauss. Entonces, el rango de A coincide con el número de posiciones pivote presentes en B.
Ejemplo práctico
Queremos calcular el rango de la matriz A.
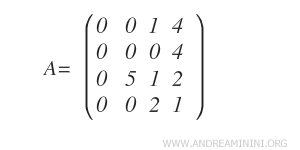
Aplicando la eliminación de Gauss, transformamos la matriz A en una matriz escalonada por filas, que denotamos por B.
La matriz B es equivalente por filas a la matriz original A.
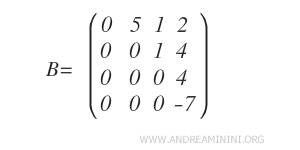
En este caso, observamos que la matriz B presenta tres posiciones pivote.
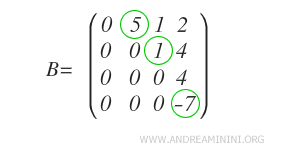
Nota. Se denomina pivote al primer elemento no nulo de una fila (leído de izquierda a derecha) que se encuentra por encima de ceros en su columna. En este contexto, no es necesario que el pivote sea igual a uno.
Podemos concluir, por tanto, que el rango de la matriz A es 3.
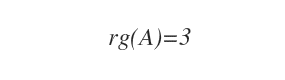
Este procedimiento permite determinar el rango de una matriz sin necesidad de recurrir al cálculo de menores.
Se trata de una alternativa eficaz y ampliamente utilizada en álgebra lineal para hallar el rango de una matriz.