Menor complementario en una matriz
El menor complementario de un elemento \( a_{ij} \) en una matriz \( A \) es el determinante de la submatriz cuadrada \( A_{(ij)} \), obtenida al eliminar la fila \( i \) y la columna \( j \) de la matriz original.

¿Cómo se calcula el menor complementario de un elemento?
Para calcular el menor complementario de \( a_{ij} \) en la matriz \( A \), se procede eliminando la fila \( i \)-ésima y la columna \( j \)-ésima.
Esto da lugar a la submatriz complementaria \( A_{(ij)} \).

El paso siguiente consiste en calcular el determinante de la submatriz \( A_{(ij)} \).
El valor de este determinante constituye el menor complementario del elemento \( a_{ij} \).
Ejemplo de cálculo
Consideremos la siguiente matriz cuadrada de orden 3:
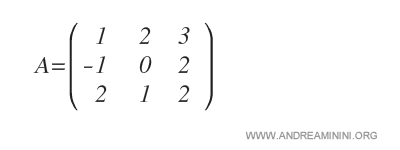
Queremos calcular el menor complementario del elemento \( a_{11} \).
Para ello, se eliminan la primera fila (\( i = 1 \)) y la primera columna (\( j = 1 \)).
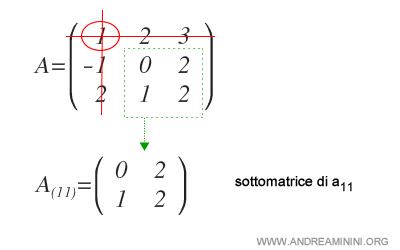
A continuación, se determina el valor del determinante de la submatriz \( A_{(11)} \).
Ese valor es el menor complementario de \( a_{11} \).
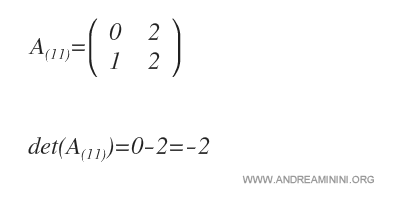
En este caso, el menor complementario es igual a 2.
Nota: Este procedimiento puede aplicarse a cualquier otro elemento de la matriz \( A \) para calcular su correspondiente menor complementario.