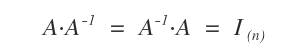Multiplicación de matrices
¿Cómo se multiplican dos matrices? En álgebra lineal, la multiplicación de matrices se realiza mediante el método fila por columna: cada fila de la primera matriz se multiplica por cada columna de la segunda.

Si Amxn es una matriz real y Bnxp otra matriz real, su producto es una matriz real Cmxp. Cada elemento cik de C se obtiene sumando los productos de los elementos correspondientes de la fila i de A con los de la columna k de B.
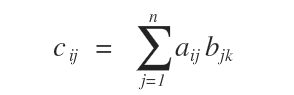
La multiplicación de matrices está definida únicamente cuando el número de columnas de la primera matriz coincide con el número de filas de la segunda.

Nota: En términos simples, para que la multiplicación esté bien definida, cada fila de A debe tener la misma cantidad de elementos que cada columna de B. Un ejemplo práctico lo ilustra a continuación.
Ejemplo de multiplicación de matrices
Veamos cómo se calcula el producto de dos matrices A y B.
La matriz A tiene dimensión 4x2, mientras que la matriz B es de tamaño 2x4.
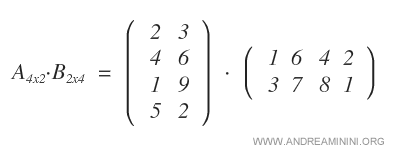
Como el número de columnas de A coincide con el número de filas de B, la multiplicación es posible.
Nota: La matriz resultante tendrá dimensión 4x4, ya que se multiplican las cuatro filas de A (i=4) por las cuatro columnas de B (k=4).

Comenzamos multiplicando cada fila de A por la primera columna de B, lo que nos da la primera columna de la matriz resultado.
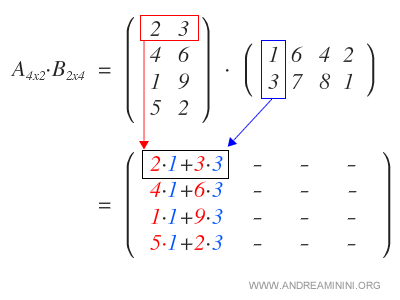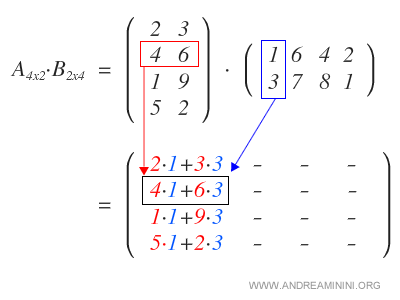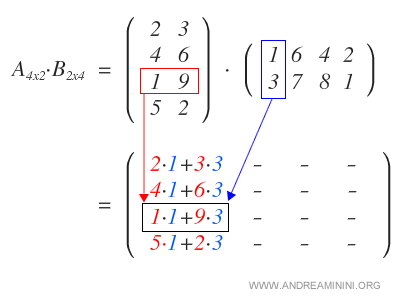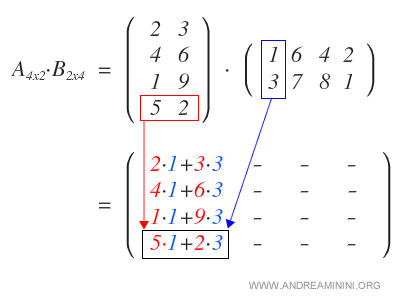
Luego multiplicamos las filas de A por la segunda columna de B para obtener la segunda columna de la matriz producto.

El proceso continúa con la tercera columna: multiplicamos cada fila de A por la tercera columna de B.

Finalmente, multiplicamos las filas de A por la cuarta columna de B para obtener la última columna de la matriz resultante.
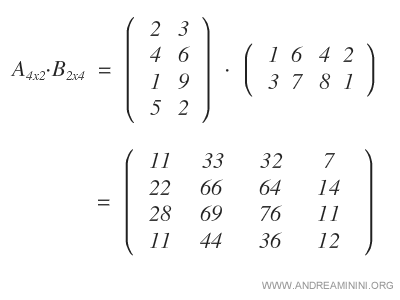
De este modo, obtenemos el producto matricial A·B.
Propiedades de la multiplicación de matrices
La multiplicación de matrices cumple con varias propiedades fundamentales:
- Propiedad asociativa: Si A∈Mmn, B∈Mnp y C∈Mpq, entonces A(BC) = (AB)C.
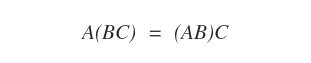
- Distributiva por la derecha: Para matrices A∈Mmn, B∈Mnp y C∈Mnp, se cumple A(B+C) = AB + AC.
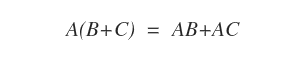
- Distributiva por la izquierda: Si A∈Mmn, B∈Mnp y C∈Mnp, entonces (A+B)C = AC + BC.
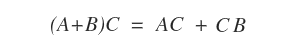
- Multiplicación por un escalar: Dado un escalar α∈R y matrices A∈Mmn, B∈Mnp, se cumple que α(AB) = (αA)B = A(αB).
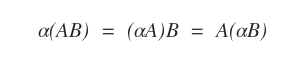
- Transposición del producto: Para A∈Mmn y B∈Mnp, se cumple que (AB)T = BTAT.
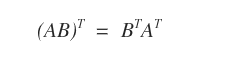
Nota: Al transponer un producto, el orden se invierte: en AB, A va primero, pero al tomar la transpuesta, aparece primero BT.
Diferencias esenciales entre matrices y números reales
La multiplicación de matrices no es conmutativa
En general, A·B no es igual a B·A.
Esto se debe a que cambiar el orden del producto suele producir matrices de dimensiones diferentes, o incluso puede hacer que el producto no esté definido.
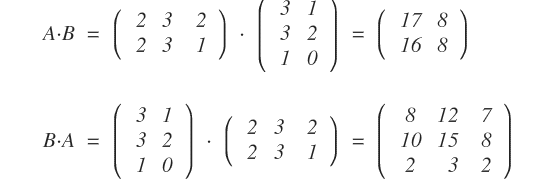
Nota: Aunque en casos especiales A·B puede coincidir con B·A (por ejemplo, si una de las matrices es la identidad), eso es poco habitual.
De hecho, a veces el producto inverso ni siquiera existe.
Por ejemplo, A puede tener tantas columnas como filas tiene B, pero si B tiene más columnas que filas tiene A, entonces el producto B·A no está definido.

En este caso, A·B está definido, pero B·A no lo está.
La multiplicación matricial no cumple la propiedad cancelativa
En el álgebra matricial, no se puede aplicar la regla de cancelación como se hace con números reales.
Si multiplicamos una matriz A por una matriz nula B, el resultado es una matriz nula.
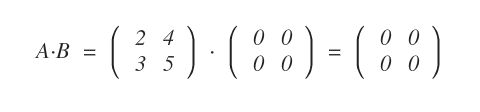
Curiosamente, también es posible que el producto de dos matrices no nulas dé como resultado una matriz nula.
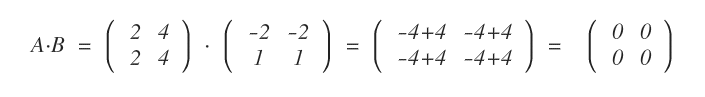
Por lo tanto, la cancelación no es válida en la multiplicación de matrices.
Las matrices y el inverso multiplicativo
En los números reales, todo número distinto de cero tiene un inverso multiplicativo: por ejemplo, 1/x, tal que x · (1/x) = 1.
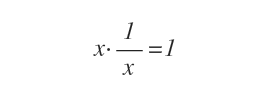
En cambio, no todas las matrices tienen inverso. Solo las matrices invertibles (o no singulares) poseen una matriz inversa A-1 tal que A · A-1 = I, donde I es la matriz identidad.
Nota: Solo las matrices invertibles tienen un inverso que, al multiplicarse por la matriz original, da como resultado la identidad.