Matriz ortogonal
Una matriz A se dice ortogonal si su inversa, A-1, coincide con su traspuesta, AT.
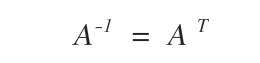
El conjunto de todas las matrices ortogonales de dimensión n se denota como On.
Nota. Solo las matrices invertibles pueden ser ortogonales; por tanto, las matrices ortogonales constituyen un subconjunto de On dentro del conjunto GLn(ℝ), que agrupa todas las matrices cuadradas invertibles de orden n.
Una propiedad clave de las matrices ortogonales es que el producto de A por su traspuesta AT es igual a la matriz identidad In.
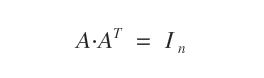
Demostración
La demostración es directa: una de las propiedades fundamentales de las matrices invertibles establece que:
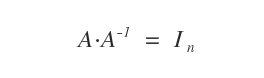
Como en las matrices ortogonales se cumple que A-1 = AT, se deduce que:
$$ AA^T = I_n $$
![]()
Un ejemplo práctico
La siguiente matriz cuadrada es un ejemplo concreto de matriz ortogonal:
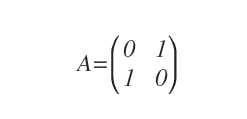
Para verificarlo, basta con calcular el producto de A por su traspuesta AT.
El resultado, A · AT, es la matriz identidad I2.
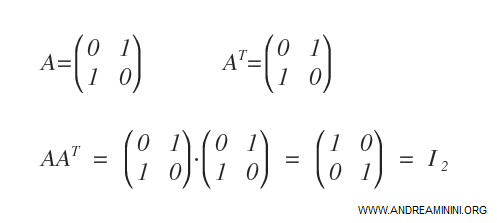
Por tanto, se confirma que AT = A-1.
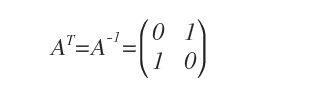
¿Por qué? Porque una de las propiedades de las matrices invertibles establece que el producto de una matriz A por su inversa A-1 es la identidad I. Así, si AAT = I y AA-1 = I, necesariamente AT = A-1.
Esto demuestra que A es efectivamente una matriz ortogonal.
Los grupos ortogonales O y SO
Las matrices ortogonales no son simples objetos algebraicos: forman una estructura con propiedades muy precisas, conocida como el grupo ortogonal, que se denota \( O(n) \). Este conjunto cumple los cuatro principios básicos del álgebra abstracta que definen un grupo matemático:
- Cierre: el producto de dos matrices ortogonales sigue siendo una matriz ortogonal;
- Asociatividad: la multiplicación de matrices cumple la propiedad asociativa;
- Elemento identidad: la matriz identidad \( I \) pertenece a \( O(n) \) y actúa como elemento neutro;
- Elemento inverso: cada matriz ortogonal \( A \) tiene como inversa su traspuesta \( A^{T} \), que también es ortogonal.
En otras palabras, el conjunto de matrices reales \( A \) que verifican
$$ A^{T}A = AA^{T} = I $$
forma un grupo bajo la multiplicación matricial.
El grupo ortogonal \( O(n) \) describe todas las isometrías lineales del espacio euclidiano, es decir, las transformaciones que preservan las distancias y los ángulos. Entre ellas se encuentran las rotaciones y las reflexiones.
Nota. En el plano, una matriz ortogonal del grupo $ O(2) $ puede representar una rotación o una reflexión. En el espacio tridimensional, las matrices de $ O(3) $ describen todas las rotaciones y simetrías espaciales que dejan invariable la forma geométrica del espacio.
En resumen, el grupo O(n) reúne todas las posibles rotaciones y reflexiones en un espacio n-dimensional.
Ahora bien, no todas estas transformaciones conservan la orientación del espacio. Las reflexiones, por ejemplo, la invierten.
Para distinguirlas, dentro de \( O(n) \) se define un subgrupo muy importante: el grupo ortogonal especial \( SO(n) \), formado por las matrices ortogonales cuyo determinante es +1:
$$ SO(n) = \{ A \in O(n) \;|\; \det(A) = +1 \} $$
Las matrices de \( SO(n) \) representan rotaciones puras, que conservan no solo las distancias y los ángulos, sino también la orientación del espacio.
Las matrices con determinante -1, en cambio, corresponden a las reflexiones, que invierten dicha orientación.
Nota. Esta diferencia es esencial en geometría y en física. El grupo \( SO(3) \) describe todas las rotaciones posibles en el espacio tridimensional, mientras que \( SO(2) \) se limita a las rotaciones del plano.