Rotación

La rotación es una transformación geométrica en el plano, en la que cada punto de una figura gira alrededor de un punto fijo llamado centro de rotación.

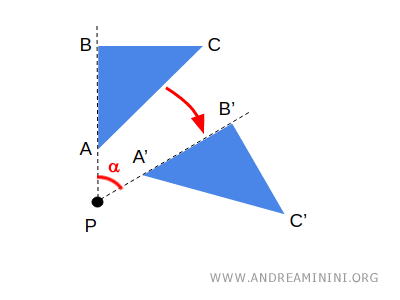
En el plano, una rotación r(P;α) con centro P y ángulo α transforma cada punto A en un nuevo punto A', de manera que el segmento PA es congruente con el segmento PA', y el ángulo APA' es igual al ángulo de rotación α, conservando el mismo sentido.

En otras palabras, una rotación desplaza los puntos (A) de una figura alrededor de un centro de rotación (P), sin modificar ni su forma ni su tamaño.

La figura resultante de una rotación es congruente con la original, lo que significa que conserva exactamente la misma forma y dimensiones. Como las distancias entre los puntos permanecen constantes, la rotación se considera una isometría.

Características de la rotación

Toda rotación está determinada por los siguientes elementos:

• El centro de rotación
• El ángulo de rotación
• El sentido de la rotación

El centro de rotación es el punto P respecto al cual gira toda la figura.

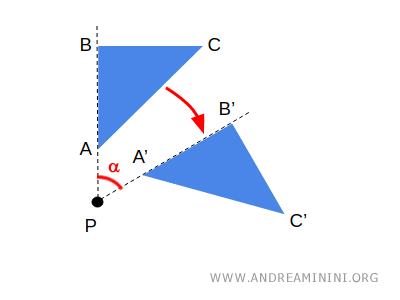
Durante la transformación, cada punto de la figura describe un arco de circunferencia con centro en P y radio constante, igual a su distancia al centro.

$$ \overline{PA} \cong \overline{PA'} $$

$$ \overline{PB} \cong \overline{PB'} $$

En consecuencia, el centro es el único punto que no cambia de posición al rotar.

El ángulo formado por cada par de puntos y el centro es congruente con el ángulo de rotación α.

$$ APA' \cong \alpha $$

$$ BPB' \cong \alpha $$

El ángulo de rotación indica cuánto gira un punto alrededor del centro.

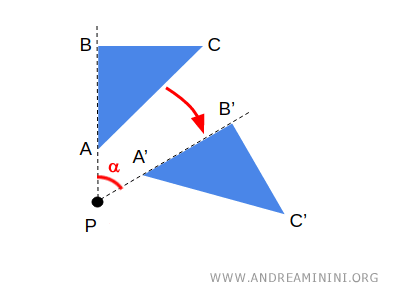
Se trata de un ángulo orientado, por lo que también se debe especificar el sentido del giro.

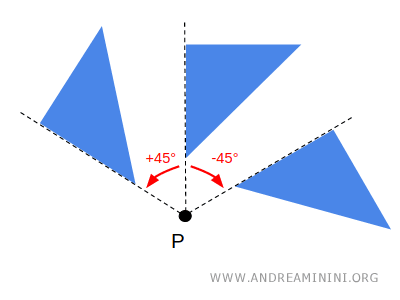
El sentido de la rotación puede ser antihorario o horario:

• Sentido antihorario
  Generalmente se representa con un ángulo positivo (por ejemplo, +45°).
• Sentido horario
  Se representa con un ángulo negativo (por ejemplo, -45°).

Ecuaciones de la rotación

La rotación de un punto \( P(x, y) \) respecto al origen \( O \) se describe mediante el siguiente sistema de ecuaciones: $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y' = x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$

Las fórmulas de rotación permiten determinar las coordenadas P'(x′,y′) de un punto P(x;y) tras ser rotado un ángulo α alrededor del origen (0,0).

Estas expresiones se simplifican especialmente cuando el ángulo de rotación es recto, es decir, α = 90°.

• Rotación de 90° en sentido horario
  Al rotar un punto P(x;y) 90° en sentido horario respecto del origen O(0;0), se obtiene el punto P'(x';y'), donde: $$ \begin{cases} x' = y \\ \\ y' = -x \end{cases} $$

  Ejemplo. Al rotar el punto A=(2;3) 90° en sentido horario (-90°), se obtiene A'=(3;-2).
  

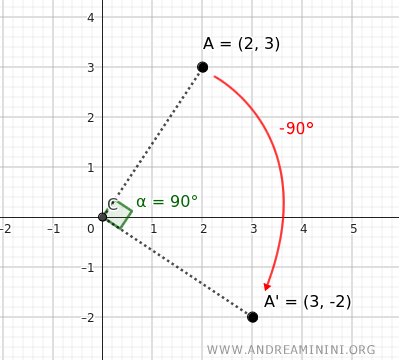
• Rotación de 90° en sentido antihorario
  Si se rota un punto P(x;y) 90° en sentido antihorario respecto del origen, se obtiene: $$ \begin{cases} x' = -y \\ \\ y' = x \end{cases} $$

  Ejemplo. Al rotar el punto A=(2;3) 90° en sentido antihorario (+90°), obtenemos A'=(-3;2).
  

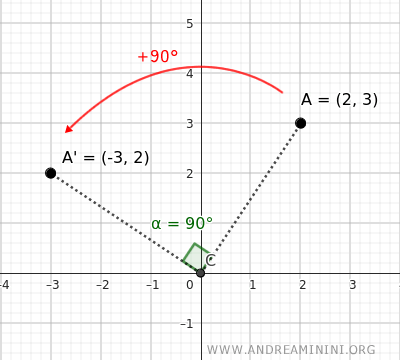
En ambos casos, las coordenadas se intercambian con el signo adecuado según el sentido del giro.

La rotación general de un ángulo α respecto al origen se expresa mediante las siguientes fórmulas:

$$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y' = x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$

Este sistema puede representarse también en forma matricial:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

Esta matriz, compuesta por funciones trigonométricas (seno y coseno), recibe el nombre de matriz de rotación.

Ejemplo. Rotar el punto A=(2;3) 45° en sentido antihorario (+45°). Aplicamos la fórmula general: $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y' = x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$ Sustituimos x = 2, y = 3: $$ \begin{cases} x' = 2 \cdot \cos \alpha - 3 \cdot \sin \alpha \\ \\ y' = 2 \cdot \sin \alpha + 3 \cdot \cos \alpha \end{cases} $$ Con α = 45°: $$ \begin{cases} x' = 2 \cdot \cos 45° - 3 \cdot \sin 45° \\ \\ y' = 2 \cdot \sin 45° + 3 \cdot \cos 45° \end{cases} $$ Como sin(45°) ≈ 0,71 y cos(45°) ≈ 0,71: $$ \begin{cases} x' = 1,42 - 2,13 \\ \\ y' = 1,42 + 2,13 \end{cases} $$ $$ \begin{cases} x' = -0,71 \\ \\ y' = 3,54 \end{cases} $$ Las coordenadas del punto A' tras la rotación de 45° son (x';y') = ( - 0,71; 3,54).

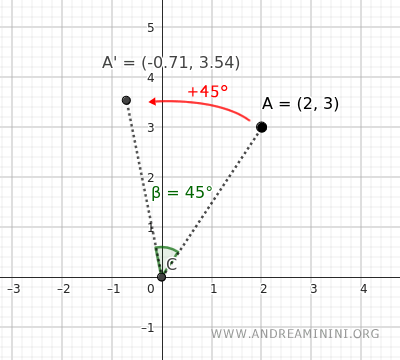
Casos especiales de rotación

En algunos casos particulares, las fórmulas de rotación se simplifican de forma notable:

• Rotación de 90° en sentido antihorario: Cuando el ángulo es $\alpha = \frac{\pi}{2}$ radianes, se cumple que $\cos \alpha = 0$ y $\sin \alpha = 1$. Las ecuaciones de la rotación se reducen a: $$ \begin{cases} x' = -y \\ y' = x \end{cases} $$

  

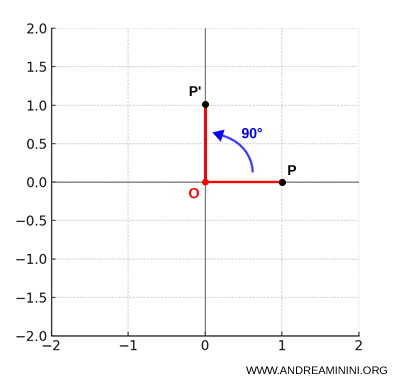
• Rotación de 90° en sentido horario: Si el ángulo es $\alpha = -\frac{\pi}{2}$, entonces $\cos \alpha = 0$ y $\sin \alpha = -1$. En este caso, las ecuaciones se simplifican a: $$ \begin{cases} x' = y \\ y' = -x \end{cases} $$

  

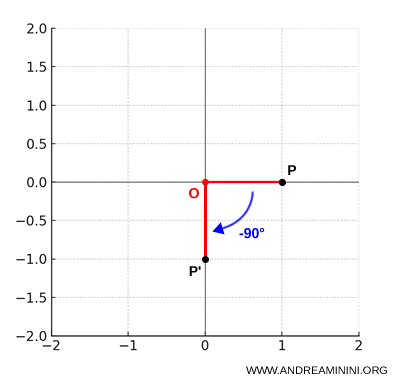
• Sin rotación o rotación completa: Si $\alpha = 0$ o $\alpha = 2\pi$, se tiene que $\cos \alpha = 1$ y $\sin \alpha = 0$. La transformación coincide entonces con la identidad: $$ \begin{cases} x' = x \\ y' = y \end{cases} $$

Demostración

Vamos a deducir paso a paso las fórmulas que describen una rotación en el plano.

Partimos de un punto P(x, y) y consideramos el segmento $ \overline{OP} $ que une el origen O con el punto P.

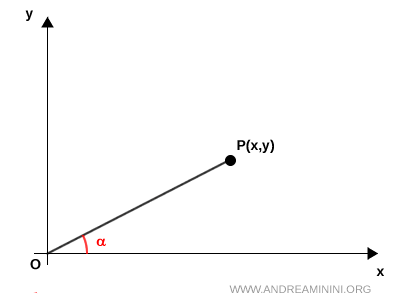
Este segmento forma un ángulo $ \alpha $ con el semieje positivo de las x.

Las coordenadas del punto $ P $ pueden expresarse en forma polar de la siguiente manera:

$$ x = \overline{OP} \cdot \cos \alpha $$

$$ y = \overline{OP} \cdot \sin \alpha $$

Aquí, $ \overline{OP} $ representa la distancia entre el origen y el punto P, es decir, la longitud del segmento.

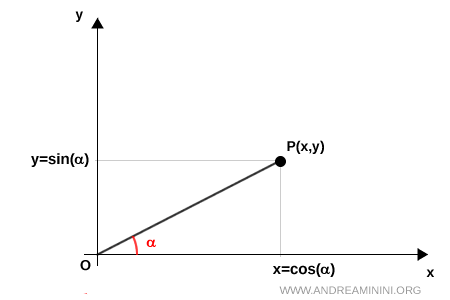
Ahora rotamos el segmento $ \overline{OP} $ un ángulo $ \beta $ en sentido antihorario, utilizando el origen O como centro de rotación.

Tras la rotación, el punto P se desplaza a una nueva posición, cuyas coordenadas denotamos como $ P'(x', y') $.

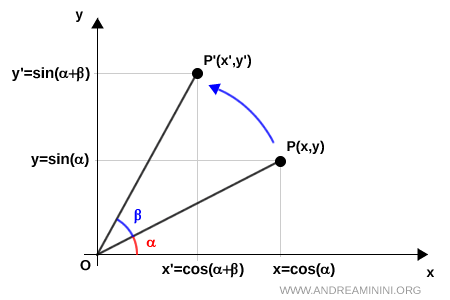
Las coordenadas del punto $ P' $ vienen dadas por:

$$ x' = \overline{OP'} \cdot \cos ( \alpha + \beta ) $$

$$ y' = \overline{OP'} \cdot \sin ( \alpha + \beta ) $$

Aplicamos ahora las fórmulas de adición de ángulos para el coseno y el seno:

$$ x' = \overline{OP'} \cdot [ \cos \alpha \cos \beta - \sin \alpha \sin \beta ] $$

$$ y' = \overline{OP'} \cdot [ \sin \alpha \cos \beta + \cos \alpha \sin \beta ] $$

Desarrollamos los productos:

$$ x' = \overline{OP'} \cos \alpha \cos \beta - \overline{OP'} \sin \alpha \sin \beta $$

$$ y' = \overline{OP'} \sin \alpha \cos \beta + \overline{OP'} \cos \alpha \sin \beta $$

Dado que la rotación es una isometría, conserva las distancias. Por tanto, $ \overline{OP} = \overline{OP'} $ y podemos hacer la sustitución:

$$ x' = \overline{OP} \cos \alpha \cos \beta - \overline{OP} \sin \alpha \sin \beta $$

$$ y' = \overline{OP} \sin \alpha \cos \beta + \overline{OP} \cos \alpha \sin \beta $$

Recordando que $ x = \overline{OP} \cos \alpha $ y $ y = \overline{OP} \sin \alpha $, sustituimos en las expresiones anteriores:

$$ x' = \underbrace{ \overline{OP} \cos \alpha }_{x} \cos \beta - \underbrace{ \overline{OP} \sin \alpha }_{y} \sin \beta $$

$$ y' = \underbrace{ \overline{OP} \sin \alpha }_{y} \cos \beta + \underbrace{ \overline{OP} \cos \alpha }_{x} \sin \beta $$

Lo que se simplifica a:

$$ x' = x \cos \beta - y \sin \beta $$

$$ y' = x \sin \beta + y \cos \beta $$

Reescribimos las expresiones para resaltar que se trata de combinaciones lineales de las coordenadas originales:

$$ x' = x \cos \beta - y \sin \beta $$

$$ y' = x \sin \beta + y \cos \beta $$

Con esto, hemos deducido las fórmulas estándar que permiten calcular las coordenadas de un punto tras una rotación alrededor del origen por un ángulo $ \beta $.

Nota. Para recuperar las coordenadas originales de un punto después de una rotación, basta con aplicar una rotación de ángulo opuesto \( -\beta \). Esto nos lleva a las siguientes expresiones: $$ \begin{aligned} x &= x' \cos(-\beta) - y' \sin(-\beta) \\ y &= x' \sin(-\beta) + y' \cos(-\beta) \end{aligned} $$ Utilizando las identidades trigonométricas \( \cos(-\beta) = \cos(\beta) \) y \( \sin(-\beta) = -\sin(\beta) \), obtenemos las fórmulas de rotación inversa: $$ \begin{aligned} x &= x' \cos \beta + y' \sin \beta \\ y &= -x' \sin \beta + y' \cos \beta \end{aligned} $$

Rotación alrededor de un punto cualquiera

La rotación de un punto respecto a un centro de rotación \((x_0, y_0)\) distinto del origen se realiza mediante la siguiente fórmula: $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$

Es decir, para rotar un punto respecto a un centro distinto del origen, como \((x_0, y_0)\), primero se traslada el sistema para que dicho punto coincida con el origen, luego se aplica la rotación, y finalmente se traslada de nuevo al sistema original.

1. Trasladar el punto al nuevo origen \((x_0, y_0)\): $$ x_{temp} = x - x_0 \\ y_{temp} = y - y_0 $$
2. Aplicar la rotación respecto al nuevo origen: $$ \begin{cases} x'_{temp} = x_{temp} \cdot \cos \alpha - y_{temp} \cdot \sin \alpha \\ y'_{temp} = x_{temp} \cdot \sin \alpha + y_{temp} \cdot \cos \alpha \end{cases} $$
3. Volver a trasladar al sistema original: $$ x' = x'_{temp} + x_0 \\ y' = y'_{temp} + y_0 $$

Combinando estas tres transformaciones geométricas, se obtiene la fórmula general para rotar un punto respecto a un centro cualquiera \((x_0, y_0)\): $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$

Esta es la fórmula general de la rotación en el plano y puede aplicarse en cualquier situación.

Por ejemplo, si se elige el origen como centro de rotación, es decir, \(x_0 = 0\) y \(y_0 = 0\), la fórmula se reduce a la rotación habitual respecto al origen.

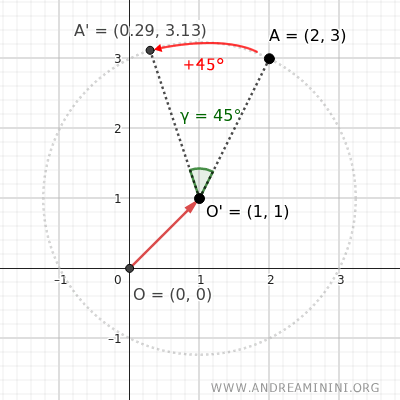
Ejemplo. Rotamos el punto A = (2;3) 45° en sentido antihorario (+45°) respecto del punto O' = (1;1), en lugar del origen O = (0;0). Aplicamos la fórmula general: $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$ Sustituimos \(x_0 = 1\) y \(y_0 = 1\): $$ \begin{cases} x' = (x - 1) \cdot \cos \alpha - (y - 1) \cdot \sin \alpha + 1 \\ \\ y' = (x - 1) \cdot \sin \alpha + (y - 1) \cdot \cos \alpha + 1 \end{cases} $$ Luego sustituimos \(x = 2\), \(y = 3\): $$ \begin{cases} x' = 1 \cdot \cos \alpha - 2 \cdot \sin \alpha + 1 \\ \\ y' = 1 \cdot \sin \alpha + 2 \cdot \cos \alpha + 1 \end{cases} $$ Sustituimos \(\alpha = 45^\circ\): $$ \begin{cases} x' = 1 \cdot 0.71 - 2 \cdot 0.71 + 1 \\ \\ y' = 1 \cdot 0.71 + 2 \cdot 0.71 + 1 \end{cases} $$ Finalmente: $$ \begin{cases} x' = 0.71 - 1.42 + 1 = 0.29 \\ \\ y' = 0.71 + 1.42 + 1 = 3.13 \end{cases} $$ Las coordenadas del punto A' tras la rotación son \(x' = 0.29\) e \(y' = 3.13\).

Rotación en el espacio

Para rotar un sólido en el espacio, se elige una recta \( r \), llamada eje de rotación, un plano \( \pi \) perpendicular a dicha recta, y un ángulo de rotación \( \alpha \).

Esta transformación asocia a cada punto \( P \) del sólido un nuevo punto \( P' \), ubicado en el mismo plano \( \pi \).

Todos los puntos situados sobre el eje \( r \) permanecen invariantes, es decir, no se desplazan durante la rotación.

Los demás puntos se mueven describiendo un arco de circunferencia dentro del plano \( \pi \), con centro en un punto \( O \) del eje \( r \), donde este intersecta el plano. El radio de la circunferencia es la distancia \( \overline{OP} \) entre el punto y el eje.

La posición del nuevo punto \( P' \) queda determinada por el ángulo de rotación \( \alpha \), que indica cuánto se ha girado alrededor del centro \( O \).

La matriz de rotación

En el plano bidimensional, una rotación de un ángulo $ \theta $ alrededor del origen puede describirse mediante una matriz ortogonal de 2×2 perteneciente al grupo especial $ SO(2) $. Este tipo de matrices permite representar transformaciones geométricas sin alterar las distancias ni los ángulos, es decir, rotaciones puras.

$$
R(\theta) =
\begin{pmatrix}
\cos\theta & -\sin\theta\\[4pt]
\sin\theta & \cos\theta
\end{pmatrix}
$$

Si aplicamos esta matriz a un vector del plano $ \mathbf{r} = \begin{pmatrix} x \\ y \end{pmatrix} $, obtenemos el vector rotado:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} =
\mathbf{r}' = R(\theta)\,\mathbf{r} =
\begin{pmatrix}
x\cos\theta - y\sin\theta\\[4pt]
x\sin\theta + y\cos\theta
\end{pmatrix}
$$

Estas son las ecuaciones clásicas de la rotación en el plano, ahora expresadas de forma compacta mediante una matriz. El sistema puede escribirse también como:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} =  \begin{pmatrix}
x\cos\theta - y\sin\theta\\[4pt]
x\sin\theta + y\cos\theta
\end{pmatrix} \Leftrightarrow  \begin{cases} x' = x \cdot \cos \theta - y \cdot \sin \theta \\ \\ y'= x \cdot \sin \theta + y \cdot \cos \theta \end{cases} $$

El módulo del vector se conserva en todo momento:

$$ d = \sqrt{ x'^2 + y'^2 } = \sqrt{ x^2 + y^2 } $$

Esto significa que la transformación corresponde a una rotación pura, sin cambios de escala ni reflexiones, propiedad fundamental de las matrices del grupo $ SO(2) $.

La matriz de rotación en el espacio tridimensional

En tres dimensiones, las rotaciones se representan mediante matrices ortogonales de 3×3 con determinante igual a 1. Dichas matrices pertenecen al grupo $ SO(3) $, el grupo ortogonal especial en tres dimensiones, que describe todas las rotaciones posibles del espacio.

La forma general de una rotación de ángulo $ \theta $ alrededor de un eje unitario \( \hat{n} = (n_x, n_y, n_z) \) es la siguiente:

$$
R(\hat{n}, \theta) =
\begin{pmatrix}
\cos\theta + n_x^2(1 - \cos\theta) & n_x n_y(1 - \cos\theta) - n_z \sin\theta & n_x n_z(1 - \cos\theta) + n_y \sin\theta \\[6pt]
n_y n_x(1 - \cos\theta) + n_z \sin\theta & \cos\theta + n_y^2(1 - \cos\theta) & n_y n_z(1 - \cos\theta) - n_x \sin\theta \\[6pt]
n_z n_x(1 - \cos\theta) - n_y \sin\theta & n_z n_y(1 - \cos\theta) + n_x \sin\theta & \cos\theta + n_z^2(1 - \cos\theta)
\end{pmatrix}.
$$

Esta expresión se conoce como la fórmula de rotación de Rodrigues, una manera compacta y elegante de describir cualquier rotación tridimensional.

Veamos ahora algunos casos particulares que se usan con frecuencia:

1] Rotación alrededor del eje x

$$
R_x(\theta) =
\begin{pmatrix}
1 & 0 & 0\\
0 & \cos\theta & -\sin\theta\\
0 & \sin\theta & \cos\theta
\end{pmatrix}.
$$

2] Rotación alrededor del eje y

$$
R_y(\theta) =
\begin{pmatrix}
\cos\theta & 0 & \sin\theta\\
0 & 1 & 0\\
-\sin\theta & 0 & \cos\theta
\end{pmatrix}.
$$

3] Rotación alrededor del eje z

$$
R_z(\theta) =
\begin{pmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0\\
0 & 0 & 1
\end{pmatrix}.
$$

Cada una de estas matrices pertenece al grupo $SO(3)$ y conserva tanto las longitudes de los vectores como los ángulos entre ellos. Su determinante es siempre $+1$, y su inversa coincide con su traspuesta, es decir, $ R^{-1} = R^{T} $. Estas propiedades garantizan que las rotaciones tridimensionales sean movimientos rígidos que no alteran la forma ni el tamaño de los cuerpos.

Observaciones

A continuación se presentan algunas consideraciones fundamentales sobre la rotación:

• La rotación es una isometría
  Dados dos puntos cualesquiera \( A \) y \( B \), y sus respectivas imágenes \( A' \) y \( B' \) bajo una rotación, la distancia entre ellos permanece inalterada. Es decir, los segmentos \( AB \) y \( A'B' \) son congruentes: \( AB \cong A'B' \).
  

  Demostración. Sean \( A \) y \( B \) puntos arbitrarios del plano, y sea \( O \) un punto fijo. Consideremos una rotación alrededor de \( O \) con ángulo \( \theta \), que transforma \( A \) y \( B \) en \( A' \) y \( B' \), respectivamente.
  
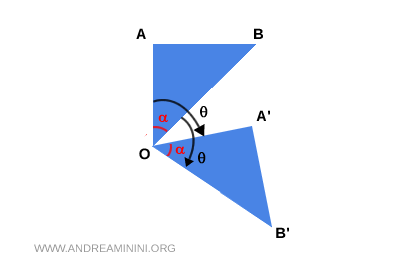
  Como la rotación conserva las distancias respecto al centro, se cumple que \( OA \cong OA' \) y \( OB \cong OB' \). Además, dado que también preserva los ángulos, se tiene que \( \angle AOB \cong \angle A'OB' \). Por tanto, los triángulos \( OAB \) y \( OA'B' \) son congruentes según el criterio de congruencia Lado-Ángulo-Lado (LAL). En consecuencia, sus lados correspondientes son iguales, lo que implica que \( AB = A'B' \). Como \( AB \) representa la distancia original entre los puntos y \( A'B' \) la distancia entre sus imágenes, se concluye que la rotación conserva las distancias. Por tanto, constituye una isometría.

• Una rotación de 0 grados o de un múltiplo de 360° equivale a la transformación identidad
  En el plano, una rotación de 0° o de cualquier múltiplo de 360° no modifica la posición de la figura, por lo que equivale a la operación identidad. En otras palabras, una rotación nula o de un número entero de vueltas completas deja la figura invariante en el plano.
  

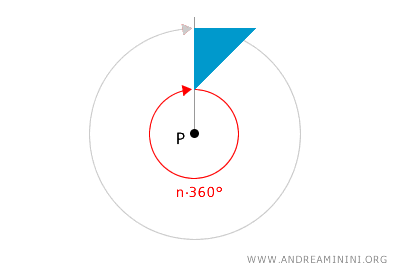
  Una figura se considera "fija" cuando todos sus puntos permanecen en la misma posición tras una transformación geométrica.

• En una rotación, el centro de rotación permanece como punto fijo
  En toda rotación, el centro P mantiene su posición en el plano. Por tanto, siempre actúa como un punto fijo.
  

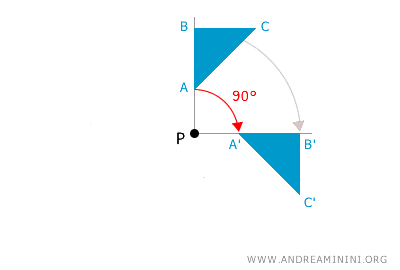
  Un punto es "fijo" si conserva su posición tras una transformación geométrica.

• La rotación no posee rectas globalmente invariantes
  En una rotación alrededor de un punto con un ángulo distinto de 0° o 360°, ninguna recta permanece globalmente invariante: cada una se transforma en otra recta ubicada en una posición diferente.

  Nota. Únicamente una rotación de un número entero de giros completos (k·360°), que en realidad equivale a la transformación identidad, deja todas las rectas no solo globalmente invariantes sino también puntualmente invariantes, ya que cada punto permanece fijo.

• La circunferencia y el círculo permanecen invariantes bajo cualquier rotación respecto a su centro
  Al rotarlos en torno a su centro, ni la circunferencia ni el círculo cambian de posición en el plano.
• Un cuadrado permanece invariante bajo rotaciones de múltiplos de 90° respecto a su centro
  Al rotar un cuadrado alrededor del punto donde se cruzan sus diagonales, la figura conserva su posición si el ángulo es un múltiplo de 90°.
• En el plano, una rotación de ±180° equivale a una simetría central
  Una rotación de 180° (media vuelta) alrededor de un punto P produce el mismo efecto que una simetría central respecto al mismo punto. Cada punto de la figura se traslada a la posición simétrica respecto a P, manteniendo la misma distancia. Así, una rotación de ±180° (±π radianes) y una simetría central en el mismo punto son transformaciones geométricas equivalentes. Esta rotación también se denomina "semivuelta" o "rotación de oposición".
  
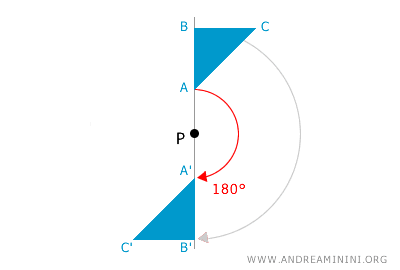
• En el espacio tridimensional, una rotación de 180° equivale a una simetría axial
  En el espacio, una rotación de 180° en torno a un eje produce el mismo efecto que una simetría axial. Cada punto del sólido se refleja con respecto al eje, como si se hubiese invertido completamente alrededor de él.
• Composición de rotaciones
  La composición de dos o más rotaciones r(P;α) y r(P;β) con el mismo centro de rotación P equivale a una única rotación con centro P y ángulo igual a la suma de los ángulos: r(P;α+β).
  

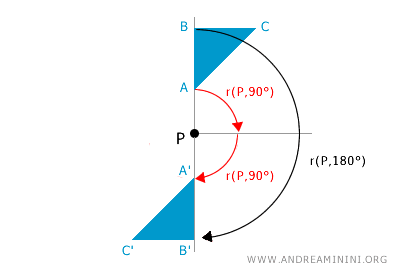
  En general, la composición de rotaciones no siempre da como resultado otra rotación, ya que si los centros son distintos, el efecto combinado puede no ser una rotación. En el siguiente ejemplo, se muestran dos rotaciones consecutivas de una misma figura con centros distintos, P y P'.
  
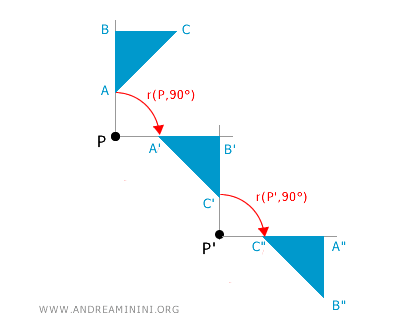
  La composición de dos rotaciones con ángulos \( \alpha_1 \) y \( \alpha_2 \), cuyos centros son puntos distintos \( P \) y \( P' \), puede dar como resultado una nueva rotación - generalmente con un centro diferente y un ángulo total igual a \( \alpha_1 + \alpha_2 \) - o bien una traslación. En consecuencia, la composición de rotaciones con centros distintos no da lugar, en general, a una nueva rotación. Por el contrario, si ambas rotaciones tienen el mismo centro \( P \), su composición es siempre una rotación alrededor de \( P \) con ángulo \( \alpha_1 + \alpha_2 \).

• Las rotaciones en el plano con un mismo centro forman un grupo conmutativo
  Si se realizan dos rotaciones sucesivas con el mismo centro P, el resultado es siempre otra rotación con centro P. Por tanto, el conjunto de rotaciones con centro fijo es cerrado. Además, el orden en que se aplican no altera el resultado: rotar primero α y luego β es equivalente a rotar primero β y luego α. Esto significa que las rotaciones en el plano cumplen la propiedad conmutativa y forman un grupo conmutativo (grupo abeliano).

Y así sucesivamente.