Teorema del Coseno

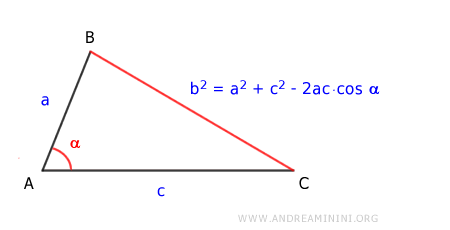
En cualquier triángulo, el cuadrado de un lado, b², es igual a la suma de los cuadrados de los otros dos lados, a² + c², menos el doble del producto de esos dos lados, 2ac, multiplicado por el coseno del ángulo α comprendido entre ellos. $$ b^2 = a^2 + c^2 - 2ac \cdot \cos \alpha $$

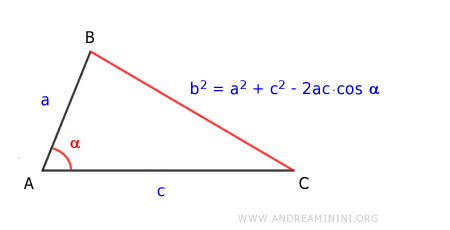
Este teorema también se conoce como el Teorema del Coseno de Carnot.

Ejemplo

Vamos a determinar la longitud del lado BC en este triángulo.

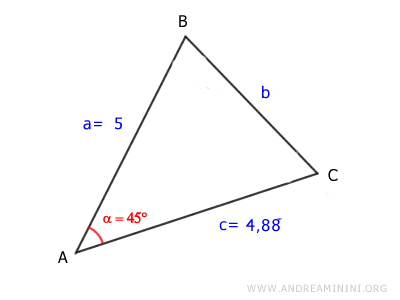
Conocemos las longitudes de los lados AB y AC, y la medida del ángulo α.

$$ \overline{AB} = 5 $$

$$ \overline{AC} = 4.88 $$

$$ \alpha = 45° $$

Aplicando el teorema del coseno, podemos calcular la longitud de BC:

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

Sustituyendo AB = 5, AC = 4.88 y α = 45°:

$$ \overline{BC}^2 = 5^2 + (4.88)^2 - 2 \cdot (5 \cdot 4.88) \cdot \cos 45° $$

$$ \overline{BC}^2 = 14.3 $$

Al extraer la raíz cuadrada en ambos miembros:

$$ \sqrt{\overline{BC}^2} = \sqrt{14.3} $$

$$ \overline{BC} = \sqrt{14.3} $$

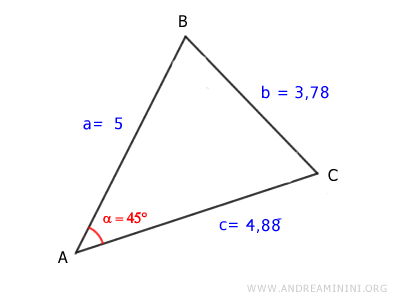
$$ \overline{BC} = 3.78 $$

Por tanto, la longitud del lado BC es 3.78.

 

La Demostración

Analicemos con detalle un triángulo cualquiera ABC.

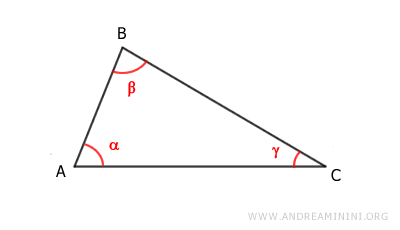
Se traza la altura h desde el vértice A, generando dos triángulos rectángulos, ABD y BCD.

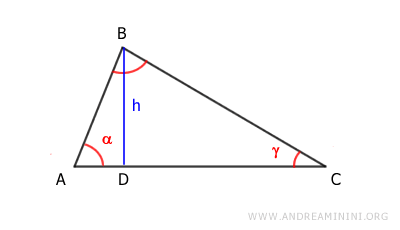
Según el primer teorema de los triángulos rectángulos, un cateto de un triángulo rectángulo es igual a la hipotenusa multiplicada por el coseno del ángulo adyacente o por el seno del ángulo opuesto.

Esto nos permite hallar las longitudes de BD y AD:

$$ \overline{BD} = \overline{AB} \cdot \sin \alpha $$

$$ \overline{AD} = \overline{AB} \cdot \cos \alpha $$

Aquí, AB es la hipotenusa del triángulo rectángulo ABD, mientras que BD y AD son sus catetos.

Dado que el segmento AC es la suma de los segmentos AD y CD:

$$ \overline{AC} = \overline{AD} + \overline{CD} $$

podemos obtener CD, el cateto del triángulo BCD, de la siguiente manera:

$$ \overline{CD} = \overline{AC} - \overline{AD} $$

$$ \overline{CD} = \overline{AC} - \overline{AB} \cdot \cos \alpha $$

Aplicando el teorema de Pitágoras, el cuadrado de la hipotenusa BC es igual a la suma de los cuadrados de los catetos en el triángulo rectángulo BCD:

$$ \overline{BC}^2 = \overline{BD}^2 + \overline{CD}^2 $$

Como CD = AC − AB · cos α,

$$ \overline{BC}^2 = \overline{BD}^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$

y BD = AB · sin α,

$$ \overline{BC}^2 = (\overline{AB} \cdot \sin \alpha)^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$

$$ \overline{BC}^2 = \overline{AB}^2 \cdot \sin^2 \alpha + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha + \overline{AB}^2 \cdot \cos^2 \alpha $$

$$ \overline{BC}^2 = \overline{AB}^2 \cdot ( \sin^2 \alpha + \cos^2 \alpha ) + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

Por la identidad fundamental de la trigonometría, se cumple que sin² α + cos² α = 1,

$$ \overline{BC}^2 = \overline{AB}^2 \cdot 1 + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

Y esta es precisamente la fórmula que queríamos demostrar.

o

Nota: Cuando el triángulo es rectángulo, el teorema del coseno se reduce al teorema de Pitágoras, ya que en un triángulo rectángulo el ángulo α es de 90° y el coseno de 90° es cero. $$ a^2 = b^2 + c^2 - 2bc \cdot \cos \alpha $$ $$ a^2 = b^2 + c^2 - 2bc \cdot \cos 90° $$ $$ a^2 = b^2 + c^2 - 2bc \cdot 0 $$ $$ a^2 = b^2 + c^2 $$

Y así sucesivamente.