Cosecante
¿Qué es la cosecante?
En trigonometría, la cosecante es una función que asigna a un ángulo α el recíproco de su seno. Se representa mediante el símbolo csc o cosec: $$ \csc \alpha = \frac{1}{\sin \alpha} $$
Desde un punto de vista geométrico, la cosecante (OA) puede interpretarse como el punto de intersección entre la recta (r), tangente en P a la circunferencia unitaria, y el eje vertical de las ordenadas.
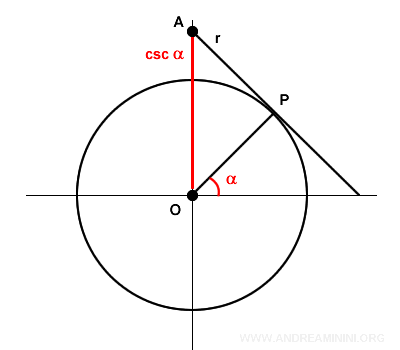
También puede visualizarse como el segmento OC, que parte del origen O, pasa por el punto P y corta la cotangente en el punto C.
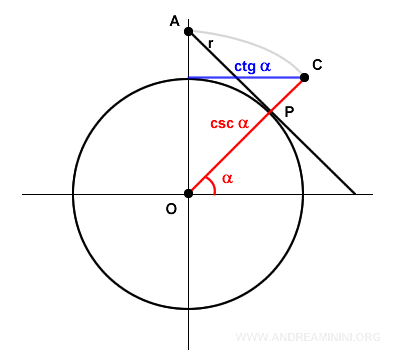
La función cosecante está definida para todos los números reales R, excepto en los puntos kπ (con k entero), ya que en ellos el seno se anula.
$$ \sec \alpha \ : \ R - k \cdot \pi \rightarrow R - (-1,1) \ \ \ \ \ \ \ \ k \in Z $$
Su codominio está formado por todos los números reales R, excluyendo el intervalo (-1,1).
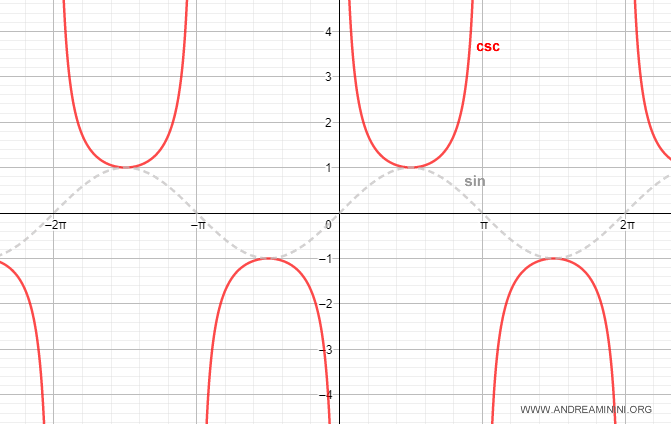
Desde el punto de vista matemático, la secante es una función impar, ya que cumple f(x) = -f(-x).
Además, es una función periódica, cuyo comportamiento se puede analizar en el intervalo (0, 2π).
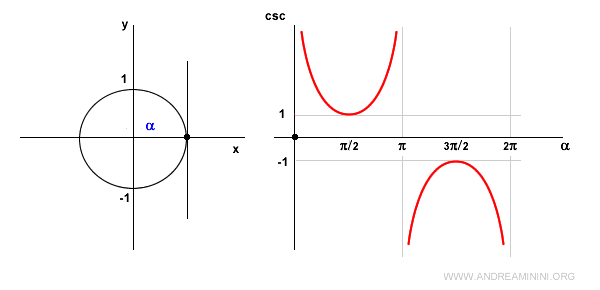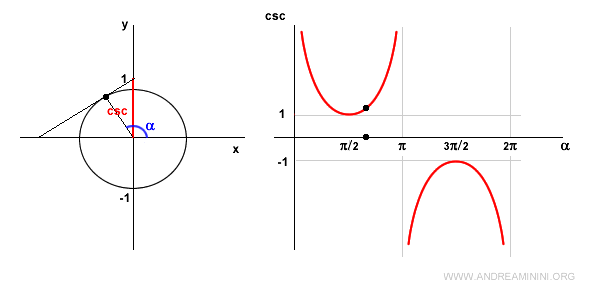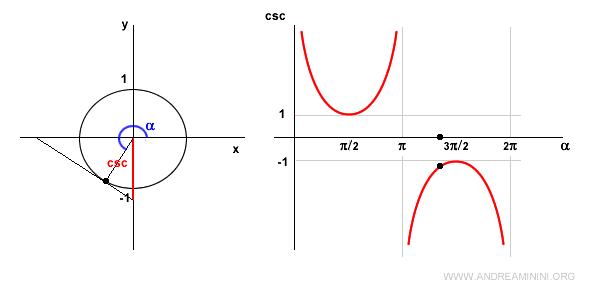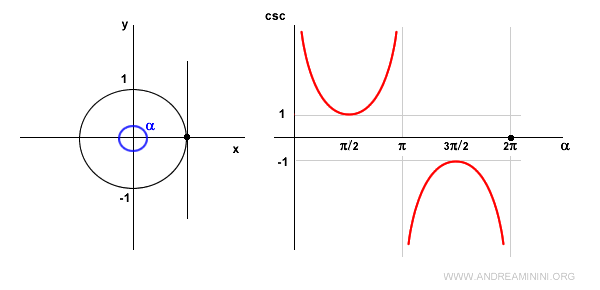
Nota: La función cosecante no está definida en los puntos kπ, donde k es un número entero. En estos valores presenta una asíntota vertical.
A continuación, se muestran algunos valores notables de la secante que conviene memorizar:
| Grados | Radianes | Secante |
|---|---|---|
| 0° | 0 | Indefinida |
| 30° | π/6 | 2 |
| 45° | π/4 | √2 |
| 60° | π/3 | (2√3)/3 |
| 90° | π/2 | 1 |
| 180° | π | Indefinida |
| 270° | 3/2π | -1 |
| 360° | 2π | Indefinida |
Demostración
Los triángulos OPB y OAP son semejantes, ya que comparten los mismos ángulos.
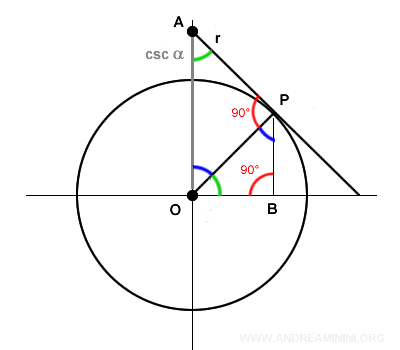
Gracias a esta semejanza, podemos establecer la siguiente proporción:
$$ \overline{OP} \ : \overline{PB} = \overline{OA} \ : \overline{OP} $$
lo que equivale a:
$$ \frac{ \overline{OP} } { \overline{PB} } = \frac{ \overline{OA} } { \overline{OP} } $$
El segmento PB representa el seno del ángulo α:
$$ \frac{ \overline{OP} } { \sin \alpha } = \frac{ \overline{OA} } { \overline{OP} } $$
Dado que el radio de la circunferencia unitaria es 1, sustituimos OP = 1:
$$ \frac{ 1 } { \sin \alpha } = \frac{ \overline{OA} } { 1 } $$
$$ \frac{ 1 } { \sin \alpha } = \overline{OA} $$
Por tanto, el segmento OA corresponde a la cosecante del ángulo α:
$$ \frac{ 1 } { \cos \alpha } = \csc \alpha $$
Así obtenemos la fórmula de la secante como el recíproco del coseno.
Demostración alternativa: Los triángulos ODC y OEP también son semejantes, ya que comparten los mismos ángulos.
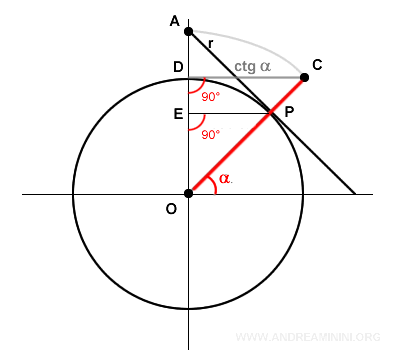
De ello se deduce la proporción entre los catetos y las hipotenusas: $$ \frac{ \overline{OE} } { \overline{OP} } = \frac{ \overline{OD} } { \overline{OC} } $$ Sabiendo que OC es la cosecante: $$ \frac{ \overline{OE} } { \overline{OP} } = \frac{ \overline{OD} } { \csc \alpha } $$ El segmento OE representa el seno: $$ \frac{ \sin \alpha } { \overline{OP} } = \frac{ \overline{OD} } { \csc \alpha } $$ Como OP y OD son radios de la circunferencia unitaria, ambos valen 1. $$ \frac{ \sin \alpha } { 1 } = \frac{ 1 } { \csc \alpha } $$ Aislando la cosecante obtenemos la fórmula deseada: $$ \csc \alpha = \frac{ 1 } { \sin \alpha } $$
Otras fórmulas de la cosecante
La cosecante de un ángulo α también puede calcularse a partir de la tangente del ángulo: $$ \csc \alpha = \sqrt{1 + \cot^2 \alpha } $$
Demostración
El radio, la cosecante y la cotangente forman un triángulo rectángulo, donde la hipotenusa es la cosecante.
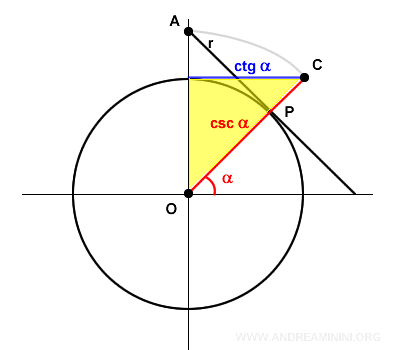
Aplicamos el teorema de Pitágoras en términos de la cotangente:
$$ \csc \alpha = \sqrt{1^2 + \cot^2 \alpha } $$
$$ \csc \alpha = \sqrt{1 + \cot^2 \alpha } $$
También puede expresarse en función del seno y el coseno, sabiendo que cot α = cos α / sin α:
$$ \csc \alpha = \sqrt{1 + \frac{\cos^2 \alpha}{\sin^2 \alpha} } $$
Gráfica de la cosecante
Cuando el ángulo es cero (α = 0), la secante no está definida porque el seno vale cero.
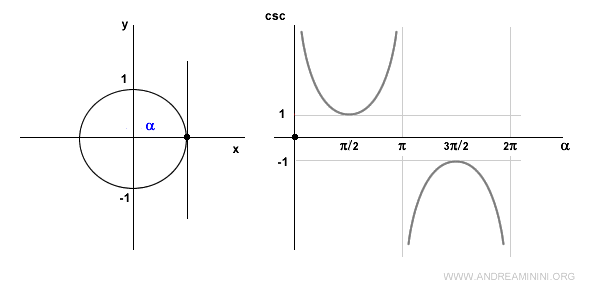
En el primer cuadrante, si α es positivo, el seno también lo es, por lo tanto la cosecante es positiva y decrece.
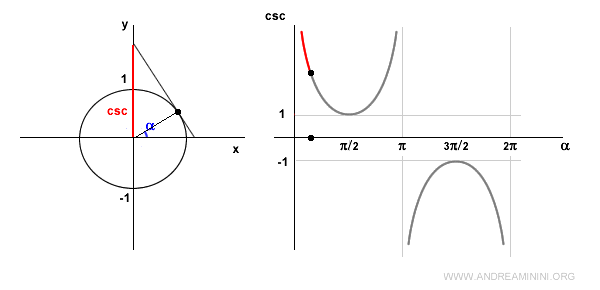
En α = π/2 (90°), la cosecante es igual a 1 porque sen(π/2) = 1.
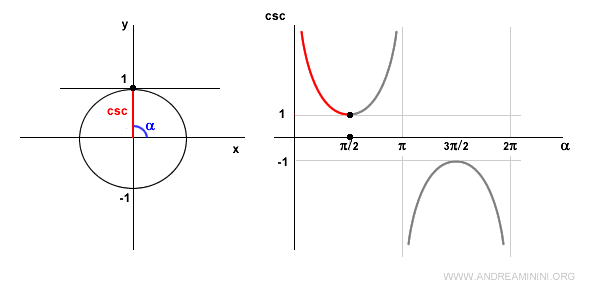
En el segundo cuadrante, el seno sigue siendo positivo, por lo que la cosecante también lo es, pero creciente.
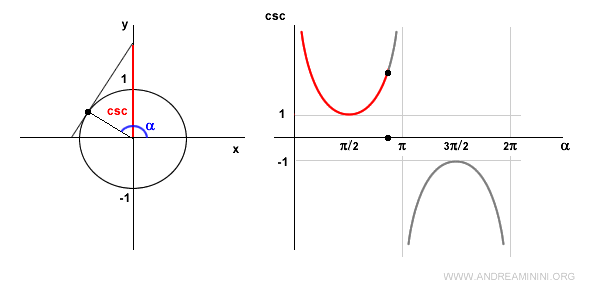
En α = π (180°), la cosecante no está definida porque sen(π) = 0, lo que genera una división por cero.
En ese punto, la recta tangente es paralela al eje y, por lo que no hay intersección.
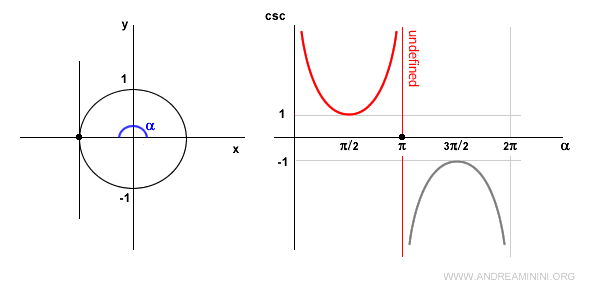
En el tercer cuadrante, donde α es negativo, el seno también lo es.
Por tanto, la cosecante resulta negativa y creciente.
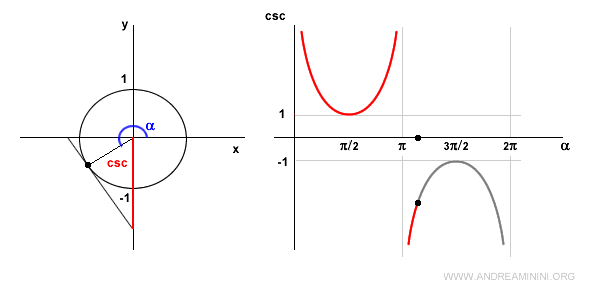
En α = 3π/2 (270°), el seno vale -1, por lo que la cosecante es igual a -1.
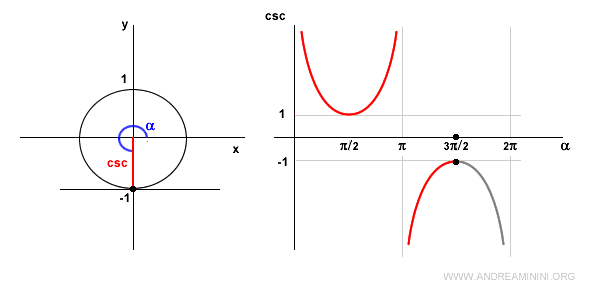
En el cuarto cuadrante, el seno es negativo, así que la cosecante también lo es, y decrece.
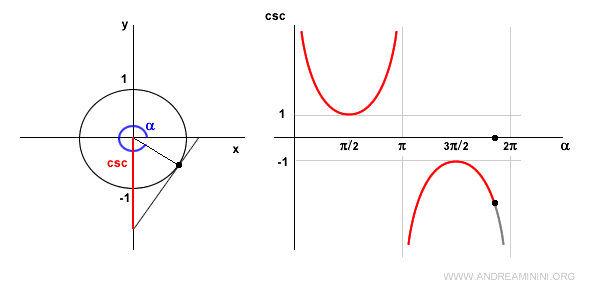
En α = 2π, volvemos al mismo caso que con α = 0: la cosecante no está definida porque sen(2π) = 0.
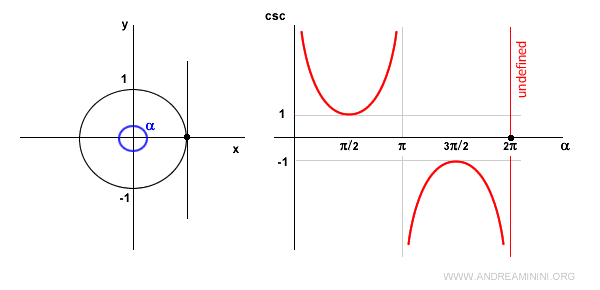
Al tratarse de una función periódica, este comportamiento se repite indefinidamente.