Ángulos Asociados en Trigonometría
Se denominan ángulos asociados a aquellos ángulos expresados en radianes que poseen los mismos valores absolutos en sus funciones trigonométricas. También se les conoce como arcos asociados.
Un ejemplo práctico
El seno de un ángulo α es igual, en valor absoluto, al seno de -α.
$$ \sin(\alpha) = |\sin(-\alpha)| $$
Por tanto, los ángulos α y -α se consideran ángulos asociados respecto de la función seno, ya que producen el mismo valor absoluto.
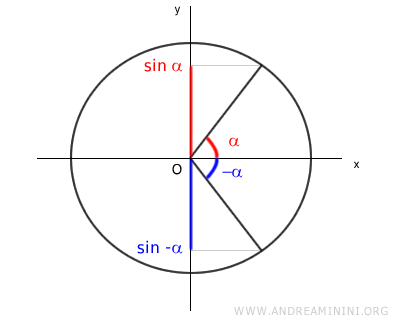
Dado que la función seno es una función impar, es decir, f(-x) = -f(x), podemos determinar el seno de -α a partir del ángulo asociado α.
$$ \sin(-\alpha) = -\sin(\alpha) $$
Nota: Los ángulos α y -α también son ángulos asociados en la función coseno. $$ \cos(\alpha) = |\cos(-\alpha)| $$ Esto significa que ambas expresiones tienen el mismo valor absoluto.
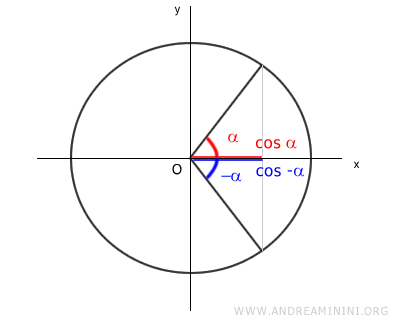
Como el coseno es una función par, es decir, f(-x) = f(x), se cumple que el coseno de -α es idéntico al coseno de α: $$ \cos(\alpha) = \cos(-\alpha) $$
¿Para qué se utilizan?
En trigonometría, los ángulos asociados permiten reducir funciones trigonométricas cuyo argumento se encuentra en cualquier cuadrante (π/2; 2π) al primer cuadrante (0; π/2).
Reducir un ángulo al primer cuadrante facilita considerablemente los cálculos.
Ejemplo: Para calcular el coseno de -20°, $$ \cos(-20°) $$, situado en el cuarto cuadrante, basta recordar que el coseno conserva su valor para ángulos opuestos. Así, podemos transformarlo al primer cuadrante: $$ \cos(-20°) = \cos(20°) $$
Fórmulas de Ángulos Asociados
Estas son las principales fórmulas de ángulos asociados en trigonometría:
| Ángulos Asociados | Fórmulas | Demostración |
|---|---|---|
| $$ \alpha \ \ , \ \ -\alpha $$ | $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \pi + \alpha $$ | $$ \sin(\pi+\alpha) = -\sin(\alpha) $$ $$ \cos(\pi+\alpha) = -\cos(\alpha) $$ $$ \tan(\pi+\alpha) = \tan(\alpha) $$ $$ \cot(\pi+\alpha) = \cot(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \pi - \alpha $$ | $$ \sin(\pi-\alpha) = \sin(\alpha) $$ $$ \cos(\pi-\alpha) = -\cos(\alpha) $$ $$ -\tan(\pi-\alpha) = \tan(\alpha) $$ $$ -\cot(\pi-\alpha) = \cot(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ 2\pi - \alpha $$ | $$ \sin(2\pi-\alpha) = -\sin(\alpha) $$ $$ \cos(2\pi-\alpha) = \cos(\alpha) $$ $$ -\tan(2\pi-\alpha) = \tan(\alpha) $$ $$ -\cot(2\pi-\alpha) = \cot(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \frac{\pi}{2} + \alpha $$ | $$ \sin(\frac{\pi}{2} + \alpha) = \cos(\alpha) $$ $$ \cos(\frac{\pi}{2} + \alpha) = -\sin(\alpha) $$ $$ \tan(\frac{\pi}{2} + \alpha) = -\cot(\alpha) $$ $$ \cot(\frac{\pi}{2} + \alpha) = -\tan(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \frac{\pi}{2} - \alpha $$ | $$ \sin(\frac{\pi}{2} - \alpha) = \cos(\alpha) $$ $$ \cos(\frac{\pi}{2} - \alpha) = \sin(\alpha) $$ $$ \tan(\frac{\pi}{2} - \alpha) = \cot(\alpha) $$ $$ \cot(\frac{\pi}{2} - \alpha) = \tan(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \frac{3\pi}{2} + \alpha $$ | $$ \sin(\frac{3\pi}{2} + \alpha) = -\cos(\alpha) $$ $$ \cos(\frac{3\pi}{2} + \alpha) = \sin(\alpha) $$ $$ \tan(\frac{3\pi}{2} + \alpha) = -\cot(\alpha) $$ $$ \cot(\frac{3\pi}{2} + \alpha) = -\tan(\alpha) $$ | ver explicación |
| $$ \alpha \ \ , \ \ \frac{3\pi}{2} - \alpha $$ | $$ \sin(\frac{3\pi}{2} - \alpha) = -\cos(\alpha) $$ $$ \cos(\frac{3\pi}{2} - \alpha) = -\sin(\alpha) $$ $$ \tan(\frac{3\pi}{2} - \alpha) = \cot(\alpha) $$ $$ \cot(\frac{3\pi}{2} - \alpha) = \tan(\alpha) $$ | ver explicación |
Y así sucesivamente.