Funciones trigonométricas
Las funciones trigonométricas establecen la relación entre la medida de un ángulo y las longitudes de los segmentos que se proyectan sobre los ejes.
Para todo ángulo α, existe un único punto P en la circunferencia, definido por su intersección con el radio correspondiente.
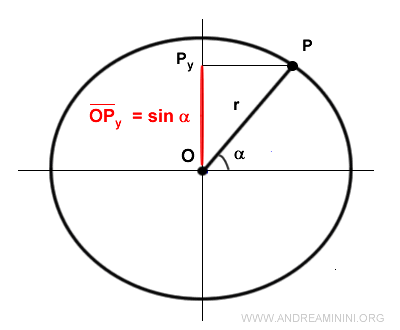
La proyección del punto P sobre el eje y determina el segmento OPy, que recibe el nombre de seno.
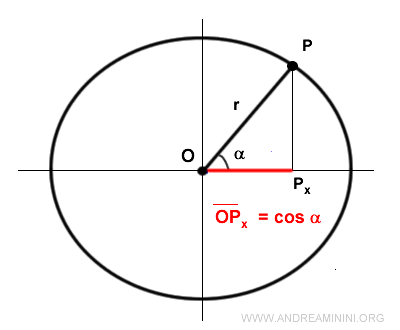
De modo similar, la proyección de P sobre el eje x da lugar al segmento OPx, conocido como coseno.
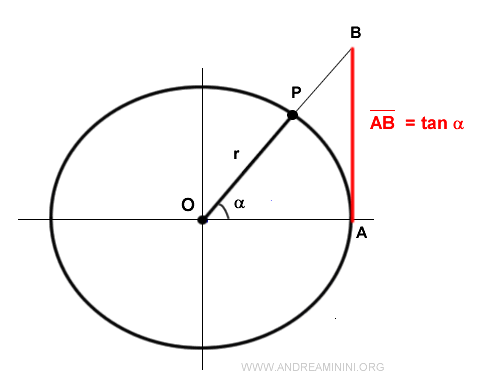
Entre las demás funciones trigonométricas de uso frecuente se encuentran la tangente y la cotangente.
Ángulos notables
A continuación se presentan algunos valores fundamentales de las funciones seno y coseno:
| Ángulo (Grados) | Ángulo (Radianes) | Seno | Coseno | Tangente | Cotangente |
|---|---|---|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{\sqrt{3}}{3} $$ | $$ \sqrt{3} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ 1 $$ | $$ 1 $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{1}{2} $$ | $$ \sqrt{3} $$ | $$ \frac{\sqrt{3}}{3} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
El coseno es una función periódica con período igual a 2π.
El período de las funciones trigonométricas
Las funciones trigonométricas se repiten a intervalos regulares, denominados períodos.
Varias de ellas comparten la misma longitud de período.
| Función | Período |
|---|---|
| $$ \sin x $$ | $$ 2 \pi $$ |
| $$ \cos x $$ | $$ 2 \pi $$ |
| $$ \sin (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \cos (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \tan x $$ | $$ \pi $$ |
| $$ \cot x $$ | $$ \pi $$ |
| $$ \tan (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
| $$ \cot (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
Y así sucesivamente.