Coseno hiperbólico (cosh)
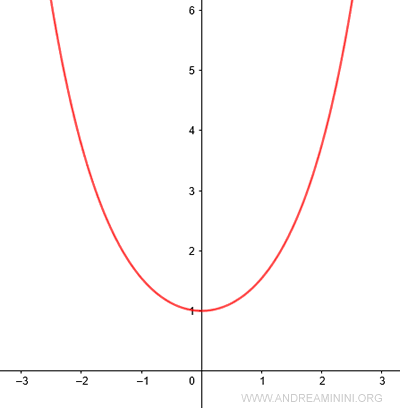
El coseno hiperbólico (cosh) es una de las funciones hiperbólicas en trigonometría. $$ \cosh(x) $$ Su dominio son todos los números reales (-∞, ∞) y su rango es [1, ∞)
A diferencia del coseno trigonométrico, el coseno hiperbólico no se define en la circunferencia unitaria, sino en la hipérbola x2 - y2 = 1.
Explicación
Representemos la hipérbola x2 - y2 = 1 en el plano cartesiano.
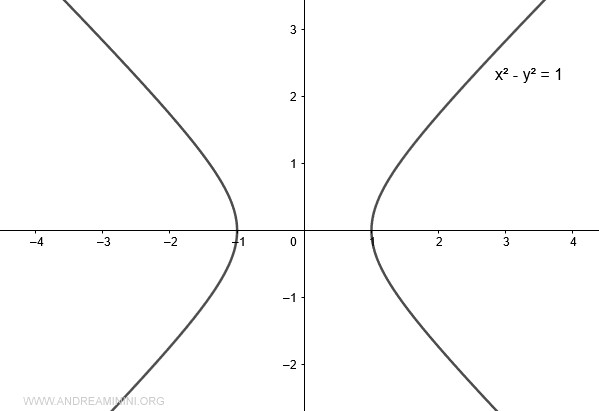
Nos fijaremos únicamente en los tramos situados en el primer y cuarto cuadrante.
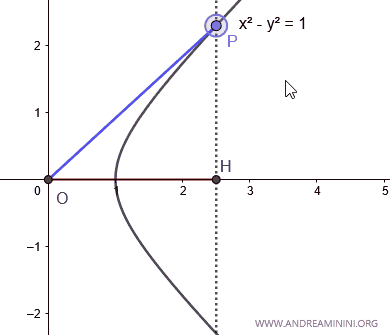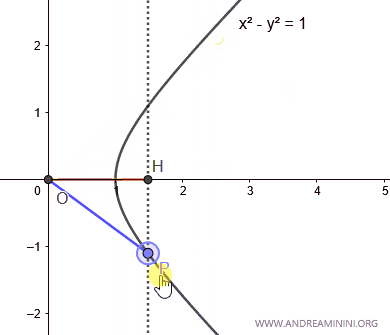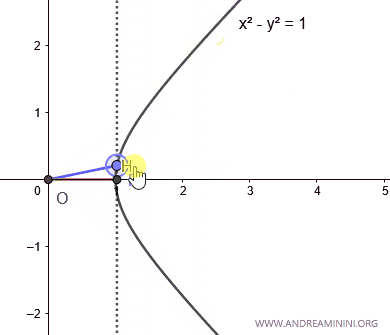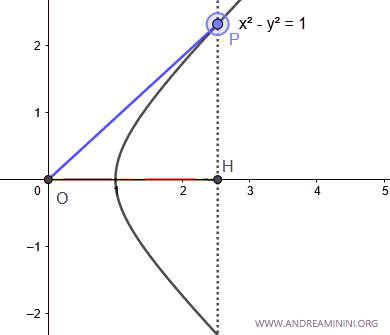
Elijamos un punto P sobre la hipérbola.
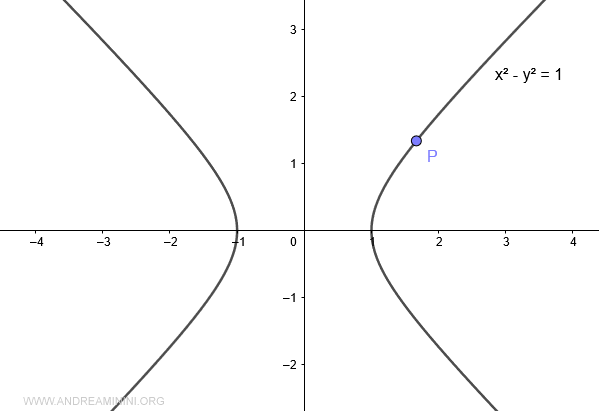
Ahora trazamos la recta que une el punto P con el origen O.
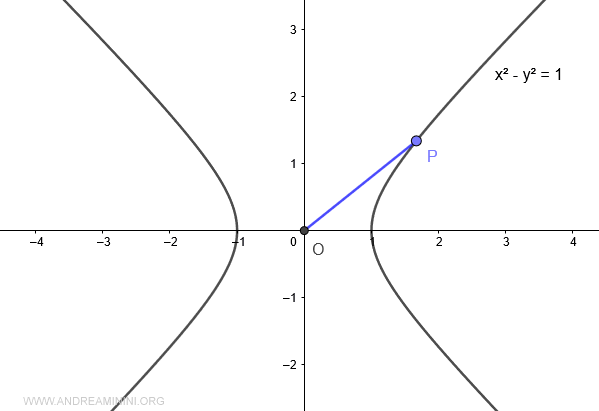
La recta OP define una abertura angular comprendida entre -π/4 y π/4 (es decir, de -45° a 45°).
El área A delimitada por el eje x, la hipérbola y la recta OP constituye el argumento (x) del coseno hiperbólico cosh(x). A este área se la denomina sector hiperbólico.
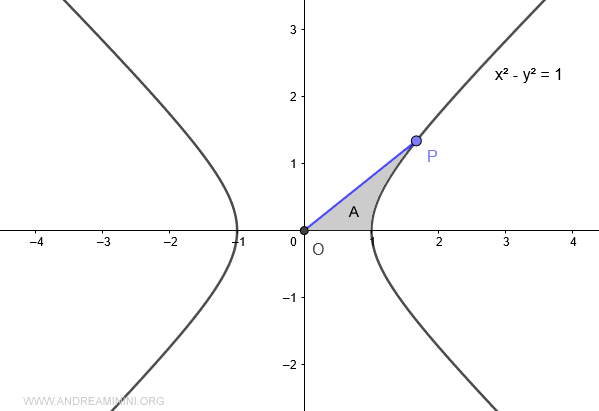
Nota: A diferencia de lo que ocurre con las funciones trigonométricas (seno, coseno, tangente, etc.), en las funciones hiperbólicas el argumento no corresponde a un ángulo.
El valor de cosh(x) se obtiene proyectando el punto P sobre el eje x.
Así, cuando el área A=0, el coseno hiperbólico vale 1.
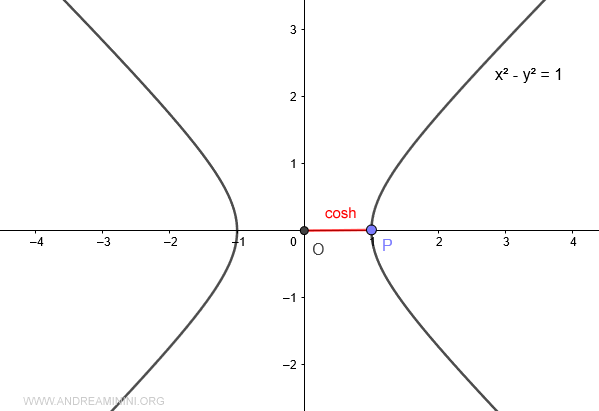
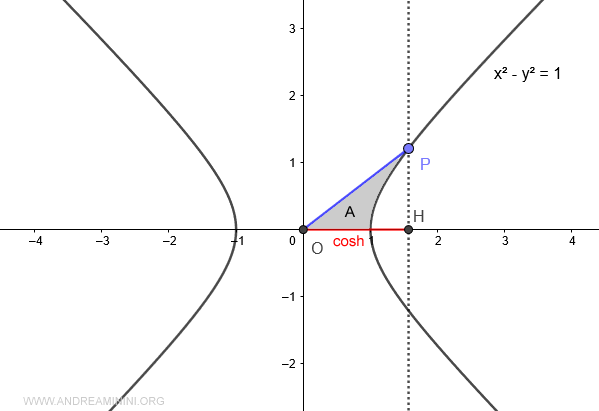
Cuando el área A>0 (mayor que cero), el coseno hiperbólico toma valores positivos.
Cuando el área A<0 (menor que cero), el coseno hiperbólico es negativo.
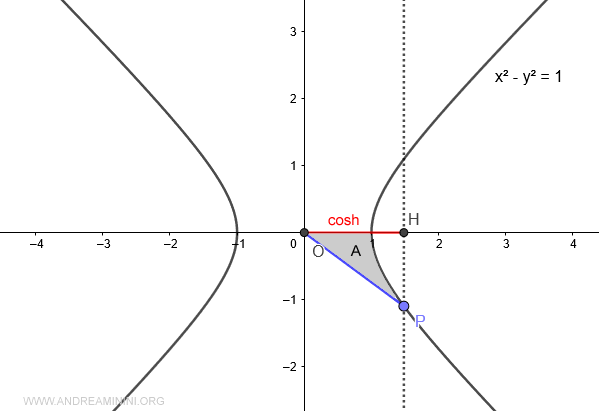
Nota: El área del sector hiperbólico es negativa cuando el punto P tiene coordenada y negativa, y positiva cuando P tiene coordenada y positiva.
El área del sector hiperbólico crece indefinidamente a medida que la coordenada x de P tiende a infinito.
Por lo tanto, el área del sector hiperbólico no está acotada y puede tomar cualquier valor real dentro del intervalo (-∞, ∞).
En cambio, el valor del coseno hiperbólico es siempre positivo y pertenece al intervalo [1, ∞).
Y así sucesivamente.