Función Coseno en Trigonometría
En la circunferencia unitaria, la función trigonométrica coseno relaciona la medida de un ángulo α con un segmento sobre el eje horizontal. Se denota como cos(α) y sus valores siempre se encuentran entre -1 y +1.
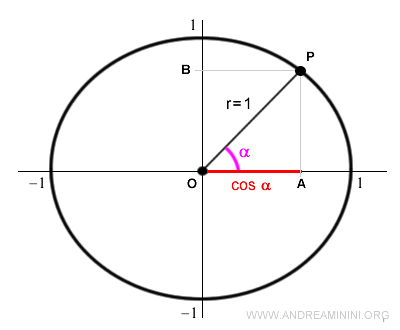
El ángulo α determina un punto P en la circunferencia unitaria.
La proyección de dicho punto P sobre el eje horizontal determina la longitud del segmento OA, conocido como el coseno de α.
Nota: El coseno puede expresarse tanto mediante el segmento OA como mediante el segmento BP, ya que son iguales: $$ \overline{OA} = \overline{BP} $$
En términos generales, el coseno de un ángulo α es la razón entre el cateto adyacente a ese ángulo y la hipotenusa en un triángulo rectángulo.
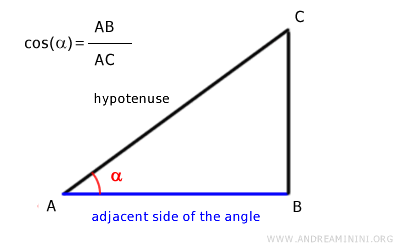
La longitud máxima que puede alcanzar este segmento equivale al radio de la circunferencia unitaria.
Dado que el radio de la circunferencia unitaria es 1 (r = 1), los valores de la función coseno siempre se encuentran en el rango comprendido entre -1 y 1.
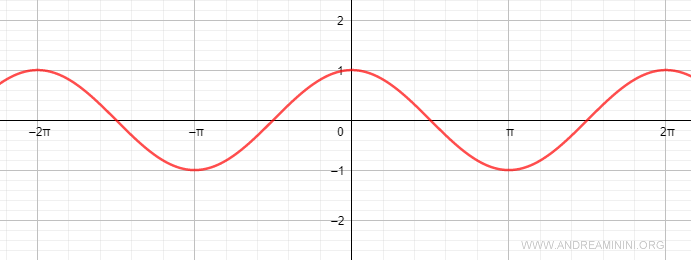
Por tanto, el recorrido (rango) de la función coseno es [-1, 1]:
$$ -1 \le \cos \alpha \le 1 $$
A continuación, se muestran algunos ángulos notables junto con sus valores de coseno:
| Ángulo (Grados) | Ángulo (Radianes) | Coseno |
|---|---|---|
| $$ 0^\circ $$ | $$ 0 $$ | $$ 1 $$ |
| $$ 15^\circ $$ | $$ \frac{\pi}{12} $$ | $$ \frac{\sqrt{6} + \sqrt{2}}{4} $$ |
| $$ 30^\circ $$ | $$ \frac{\pi}{6} $$ | $$ \frac{\sqrt{3}}{2} $$ |
| $$ 45^\circ $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ |
| $$ 60^\circ $$ | $$ \frac{\pi}{3} $$ | $$ \frac{1}{2} $$ |
| $$ 90^\circ $$ | $$ \frac{\pi}{2} $$ | $$ 0 $$ |
| $$ 180^\circ $$ | $$ \pi $$ | $$ -1 $$ |
| $$ 270^\circ $$ | $$ \frac{3\pi}{2} $$ | $$ 0 $$ |
El coseno es una función periódica cuyo periodo es 2π.
Esto significa que 2π corresponde a una vuelta completa alrededor de la circunferencia unitaria, es decir, a un ángulo de 360°.
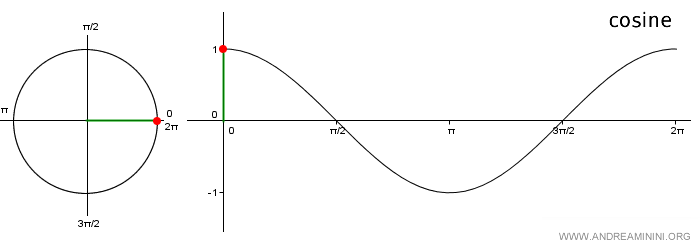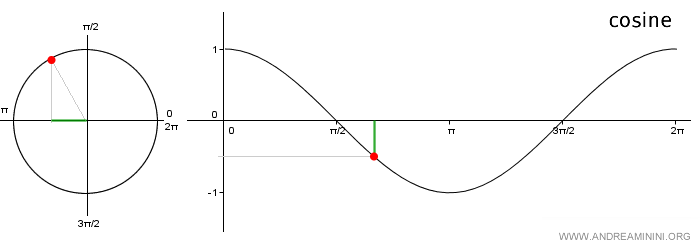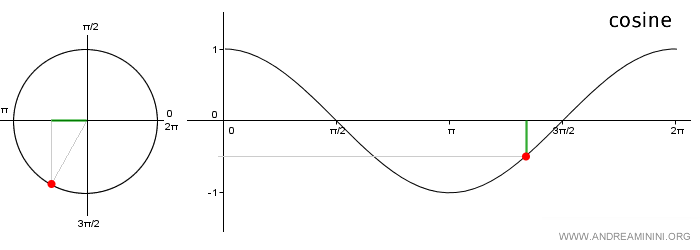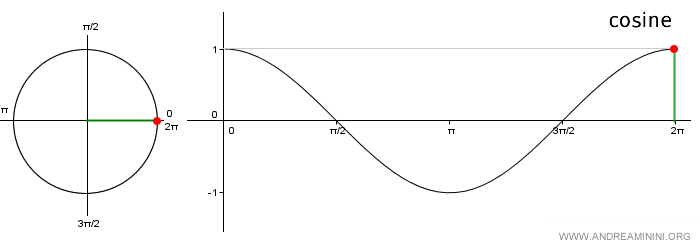
Nota: El gráfico de la función coseno se conoce como onda cosenoidal. Se construye representando en el eje x los ángulos y, en el eje y, los valores correspondientes del coseno obtenidos de la circunferencia unitaria. Al ser una función periódica, basta con estudiar el intervalo [0, 2π].
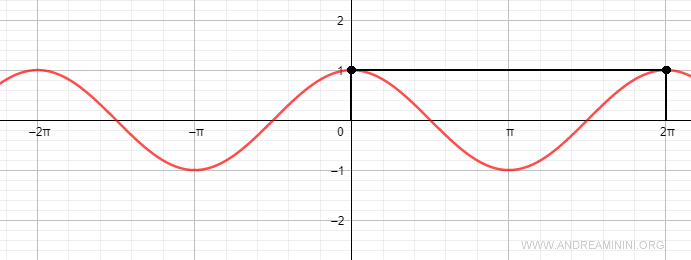
Si a un ángulo α se le suman una o más vueltas completas (2π), se regresa al mismo punto P en la circunferencia unitaria y la función coseno devuelve el mismo valor.
$$ \cos \alpha = \cos \bigl( \alpha + n \cdot 2\pi \bigr) $$
Por ejemplo, tanto cos(0) como cos(0 + 2π) tienen el mismo valor, que es 1.
Nota: Desde el punto de vista matemático, el coseno es una función par, porque $$ \cos(-\alpha) = \cos \alpha $$ Esto se puede entender observando la circunferencia unitaria: un ángulo orientado α y su opuesto -α tienen la misma proyección sobre el eje x.
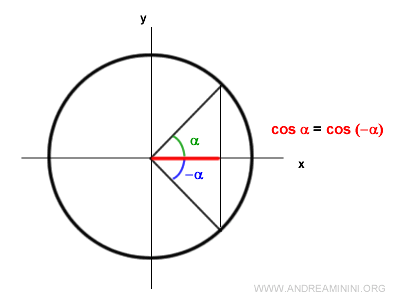
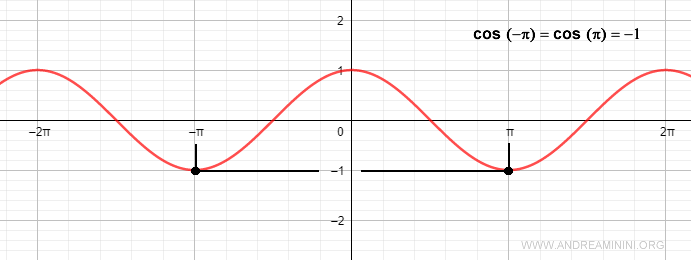
Por eso, la función coseno es simétrica respecto del eje y. Por ejemplo, el coseno de π es -1, y el coseno de -π también es -1.
Origen de la Palabra «Coseno»
El término latino cosinus fue introducido por el matemático y astrónomo inglés Edmund Gunter en el siglo XVII.
La palabra “coseno” surgió mucho tiempo después que el término “seno”.
Aunque tanto los árabes como los griegos conocían el concepto de coseno, nunca le asignaron un nombre específico.
Y así sucesivamente.