Función Seno en Trigonometría
En la circunferencia unitaria, la función trigonométrica seno relaciona la medida de un ángulo α con un segmento vertical. Se denota habitualmente como sin(α), o sen(α) en textos en español e italiano, y sus valores se encuentran comprendidos entre -1 y +1.
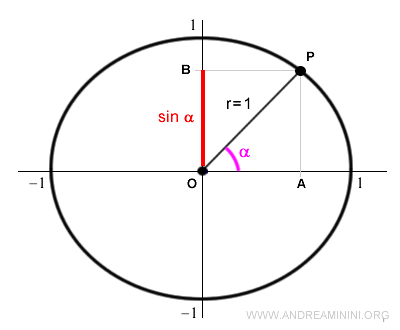
El ángulo α determina un punto P sobre la circunferencia unitaria.
La proyección de ese punto P sobre el eje vertical define la longitud del segmento OB, que corresponde al seno de α.
Nota: El valor del seno puede medirse indistintamente mediante el segmento OB o el segmento AP, dado que $$ \overline{OB} = \overline{AP} $$
En términos generales, el seno de un ángulo α es la razón entre el cateto opuesto al ángulo y la hipotenusa en un triángulo rectángulo.
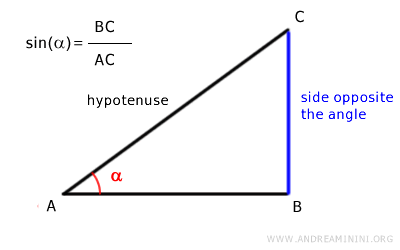
La longitud máxima de este segmento coincide con el radio de la circunferencia unitaria.
Como la circunferencia unitaria tiene radio igual a 1 (r = 1), los valores que puede tomar la función seno están comprendidos entre -1 y +1.
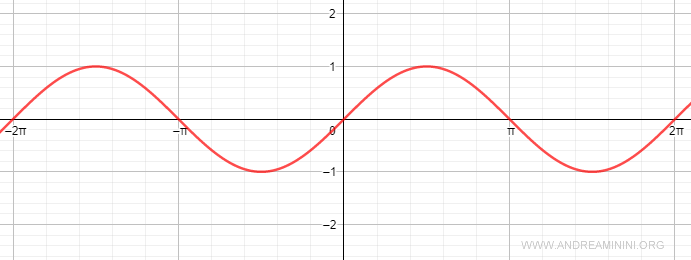
Por tanto, el recorrido (rango) de la función seno es [-1, 1]:
$$ -1 \leq \sin \alpha \leq 1 $$
A continuación, se muestran algunos ángulos notables y sus valores de seno:
| Ángulo (Grados) | Ángulo (Radianes) | Seno |
|---|---|---|
| $$ 0^\circ $$ | $$ 0 $$ | $$ 0 $$ |
| $$ 30^\circ $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ |
| $$ 45^\circ $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ |
| $$ 60^\circ $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ |
| $$ 90^\circ $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ |
| $$ 180^\circ $$ | $$ \pi $$ | $$ 0 $$ |
| $$ 270^\circ $$ | $$ \frac{3\pi}{2} $$ | $$ -1 $$ |
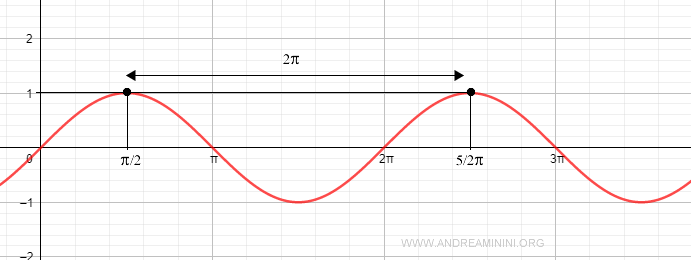
La función seno es una función periódica con un período de 2π.
Esto significa que 2π equivale a una vuelta completa alrededor de la circunferencia unitaria, es decir, a un ángulo de 360°.
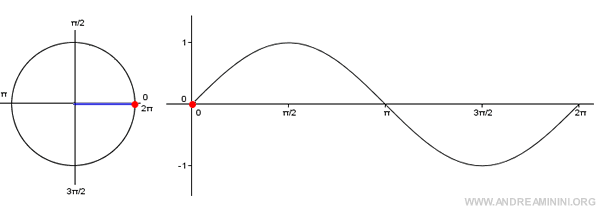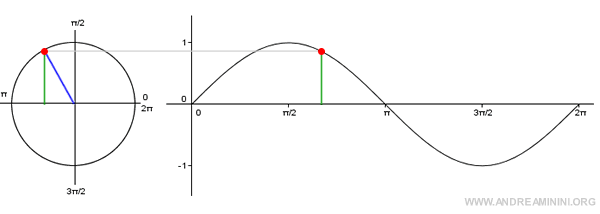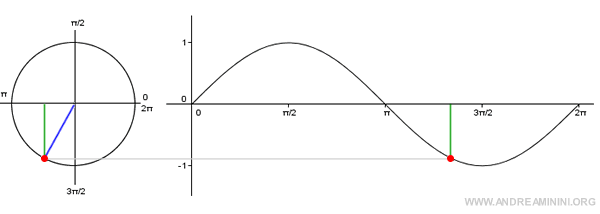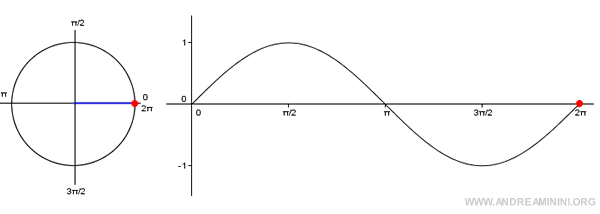
Nota: El gráfico de la función seno recibe el nombre de sinusoide. Para representarla, se sitúan en el eje x los ángulos y en el eje y sus valores de seno. Dado que es una función periódica, basta con considerar el intervalo [0, 2π].
Si a un ángulo α se le suman una o varias vueltas completas (2π), se alcanza nuevamente el mismo punto P sobre la circunferencia unitaria, y la función seno devuelve el mismo valor.
$$ \sin \alpha = \sin ( \alpha + n \cdot 2 \pi ) $$
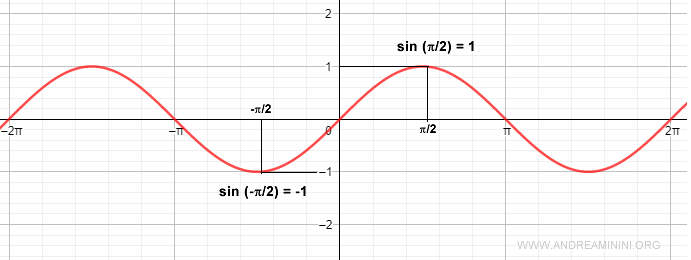
Por ejemplo, tanto sin(π/2) como sin(π/2 + 2π) tienen valor 1.
Nota: Matemáticamente, el seno es una función impar, ya que $$ \sin(-\alpha) = -\sin \alpha $$ Es decir, el seno de un ángulo orientado α y el de su opuesto -α tienen el mismo valor absoluto, pero signo contrario.
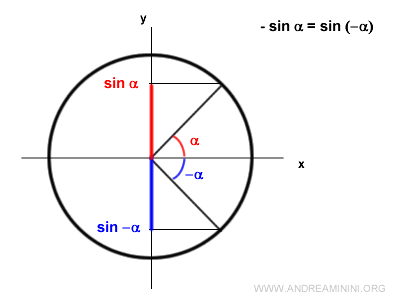
Por ejemplo, el seno de π/2 es +1, mientras que el seno de -π/2 es -1.
Origen de la Palabra “Seno”
La palabra “seno” proviene del término indio jiiva, empleado por el matemático y astrónomo Aryabhata en el siglo V d. C. para referirse a las semicuerdas de una circunferencia.
Posteriormente, el término se tradujo al árabe como jaib, que significa “pliegue” o “bolsillo”.
En Europa, la palabra árabe “jaib” se tradujo al latín como sinus, cuyo significado es “curvatura” o “pliegue”, lo que dio lugar finalmente al término “seno”.