Tangente
En la circunferencia unitaria, la función trigonométrica tangente de un ángulo α se define como el cociente entre el seno y el coseno de dicho ángulo: $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ y suele abreviarse como tan o tg.
El término “tangente” proviene del latín tangere, que significa “tocar”.
Geométricamente, la tangente se representa como un segmento perpendicular al eje x, que parte del punto C y corta la prolongación del segmento OP.
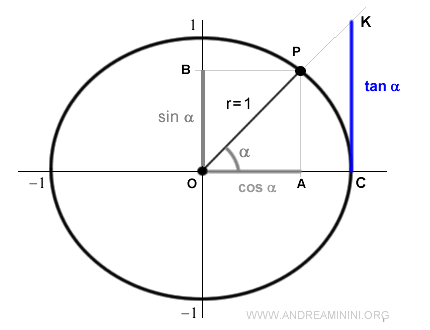
Demostración. Para un ángulo dado α, se forman dos triángulos semejantes: OAP y OCK. A partir de la semejanza, se cumple la siguiente proporción entre segmentos: $$ \overline{KC} : \overline{PA} = \overline{OC} : \overline{OA} $$ que se puede expresar como: $$ \frac{\overline{KC}}{\overline{PA}} = \frac{\overline{OC}}{\overline{OA}} $$ En la circunferencia unitaria, el radio es 1, por lo que se sustituye OC = 1: $$ \frac{\overline{KC}}{\overline{PA}} = \frac{1}{\overline{OA}} $$ Despejando KC: $$ \overline{KC} = \frac{\overline{PA}}{\overline{OA}} $$ Aquí, PA representa el seno de α, y OA representa el coseno de α. Por tanto: $$ \overline{KC} = \frac{\sin \alpha}{\cos \alpha} $$ Dado que $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ queda demostrado que el segmento KC es igual al valor de la tangente del ángulo α.
La tangente es una función periódica con un periodo de π.
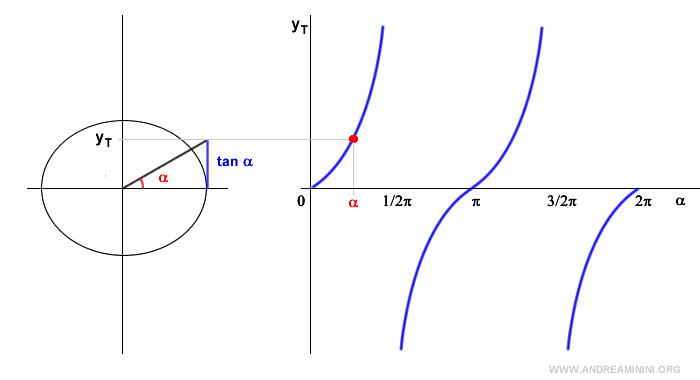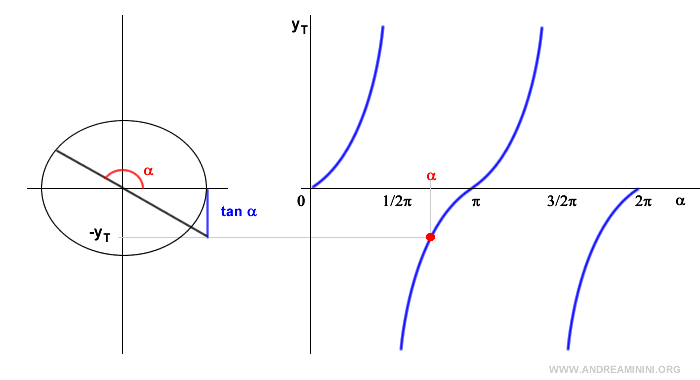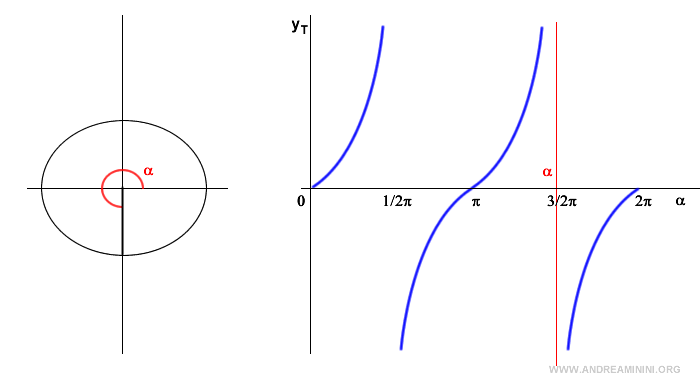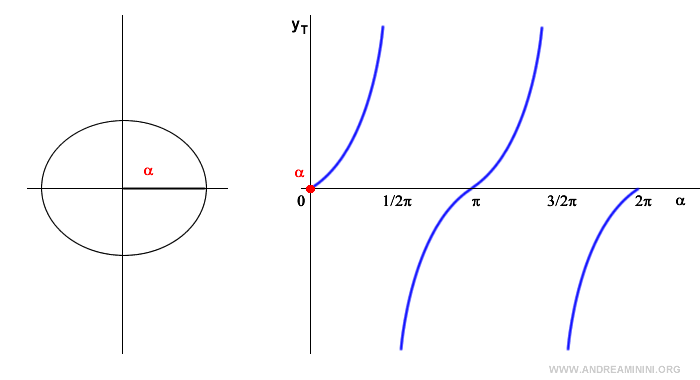
Nota. En el primer cuadrante, la tangente es positiva y tiende a infinito cuando el ángulo se aproxima a 90°. En 90°, la tangente no está definida porque el coseno es cero. En el segundo cuadrante, la tangente es negativa ya que el coseno es negativo y el seno positivo. En el tercer cuadrante, la tangente vuelve a ser positiva porque tanto el seno como el coseno son negativos. En 270°, la tangente otra vez es indefinida. En el cuarto cuadrante, la tangente es negativa, pues el seno es negativo y el coseno positivo.
La tangente no está definida en $$ \frac{\pi}{2} $$ (90°) ni en $$ \frac{3\pi}{2} $$ (270°).
En estos puntos se producen asíntotas verticales.
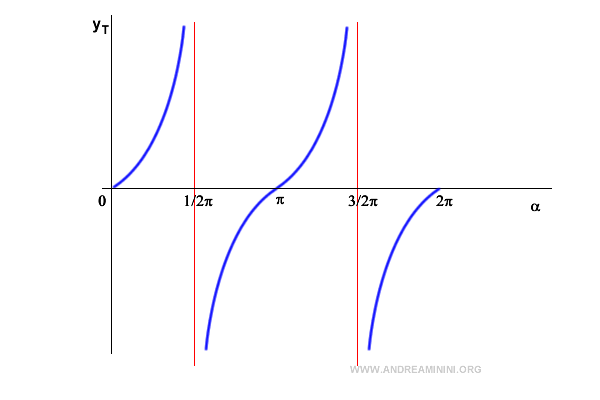
Como función periódica, la tangente presenta infinitas asíntotas verticales en los puntos:
$$ \frac{\pi}{2} + k \cdot \pi \quad \text{con } k \in \mathbb{Z} $$
Por lo tanto, el dominio de la función tangente está formado por todos los números reales, salvo aquellos valores en los que no está definida:
$$ \mathbb{R} \setminus \left\{ \frac{\pi}{2} + k \cdot \pi \right\} $$
Su recorrido, en cambio, abarca todos los números reales:
$$ \tan \alpha : \; \mathbb{R} \setminus \left\{ \frac{\pi}{2} + k \cdot \pi \right\} \longrightarrow (-\infty, +\infty) $$
A diferencia del seno y el coseno, la tangente puede adoptar cualquier valor real.
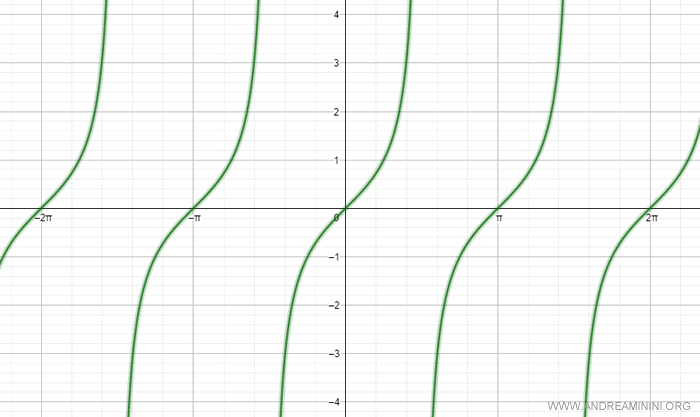
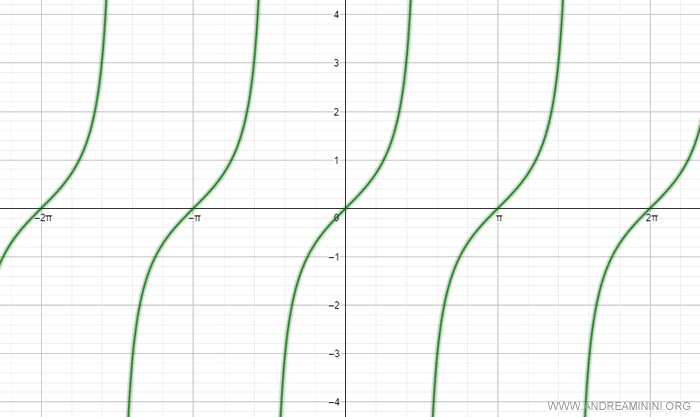
Nota. El gráfico completo de la función tangente se denomina tangentoide.
La tangente es una función periódica que se repite cada π (o 180°):
$$ \tan \alpha = \tan(\alpha + n \cdot \pi) $$
No es una función continua, ya que presenta infinitas discontinuidades asociadas a sus asíntotas verticales.
La tangente no está definida en $$ \frac{\pi}{2} $$ ni en ningún ángulo periódico de la forma:
$$ \alpha = \frac{\pi}{2} \pm n \cdot \pi $$
Nota. El cociente seno/coseno se vuelve indefinido cuando el denominador es cero, es decir, cuando el coseno es cero. Esto ocurre en $$ \frac{\pi}{2} $$ y en todos los valores obtenidos sumando múltiplos enteros de π a $$ \frac{\pi}{2} $$, es decir: $$ \cos\left(\frac{\pi}{2} + k \cdot \pi\right), \quad k \in \mathbb{Z} $$
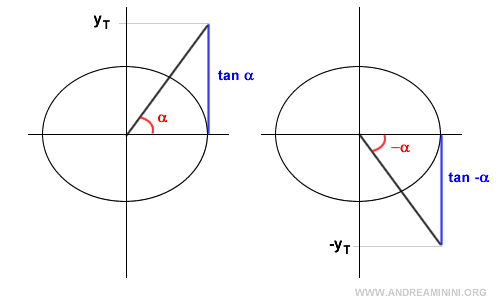
La tangente es una función impar, lo que significa que:
$$ \tan(-\alpha) = -\tan(\alpha) $$
La tangente de un ángulo orientado α y la de su opuesto -α tienen el mismo valor absoluto pero signos opuestos.
Ángulos Notables
Estos son algunos valores notables de la función tangente:
| Ángulo (Grados) | Ángulo (Radianes) | Tangente |
|---|---|---|
| $$ 0^\circ $$ | $$ 0 $$ | $$ 0 $$ |
| $$ 30^\circ $$ | $$ \frac{\pi}{6} $$ | $$ \frac{\sqrt{3}}{3} $$ |
| $$ 45^\circ $$ | $$ \frac{\pi}{4} $$ | $$ 1 $$ |
| $$ 60^\circ $$ | $$ \frac{\pi}{3} $$ | $$ \sqrt{3} $$ |
| $$ 90^\circ $$ | $$ \frac{\pi}{2} $$ | $$ \nexists $$ |
| $$ 180^\circ $$ | $$ \pi $$ | $$ 0 $$ |
| $$ 270^\circ $$ | $$ \frac{3\pi}{2} $$ | $$ \nexists $$ |
La tangente es una función periódica con periodo π.
Función Inversa de la Tangente
La tangente, en principio, no es invertible porque no es una función biyectiva.
Sin embargo, si se restringe el dominio al intervalo [-π/2, π/2], la tangente se convierte en una función biyectiva.
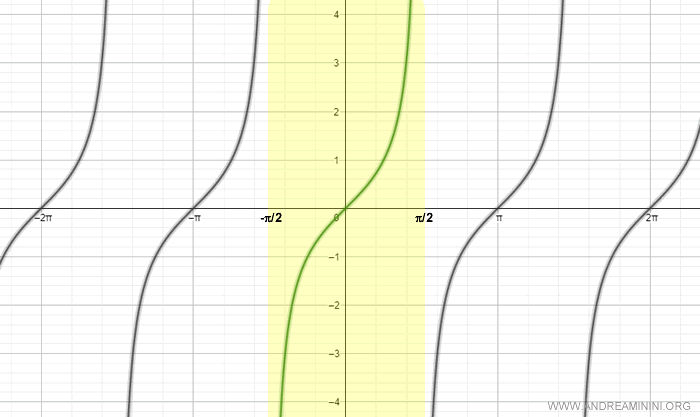
Por tanto, en el intervalo [-π/2, π/2], la tangente es invertible.
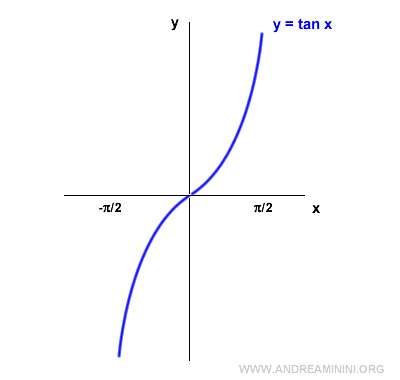
Para trazar el gráfico de la función tangente inversa, se rota el gráfico de la tangente 90° en sentido antihorario.
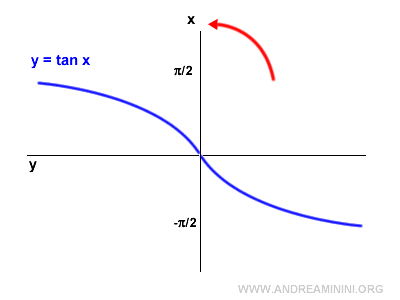
Después, se refleja horizontalmente.
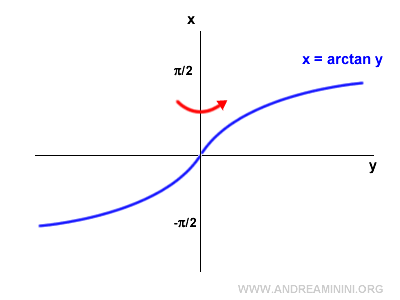
La inversa de la tangente se conoce como arcotangente (arctan).
Nota. La tangente puede invertirse en otros intervalos siempre que la función permanezca biyectiva. Por ejemplo, también es invertible en el intervalo [π/2, 3π/2].
Origen del Término «Tangente»
La palabra “tangente” fue introducida por el matemático y físico danés Thomas Fincke en el siglo XVI, originalmente en el contexto de los relojes de sol.
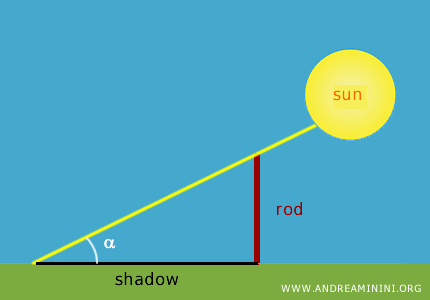
En un reloj de sol, una varilla (gnomon) proyecta una sombra sobre el suelo formando un ángulo α.
La relación entre la longitud de la varilla y la longitud de su sombra corresponde a la tangente del ángulo α.
Y así sucesivamente.