Relación entre la tangente y la pendiente de una recta
La pendiente de una recta y = mx + q coincide con la tangente del ángulo α que forma dicha recta con el eje horizontal x: $$ m = \tan \alpha$$
De manera visual:
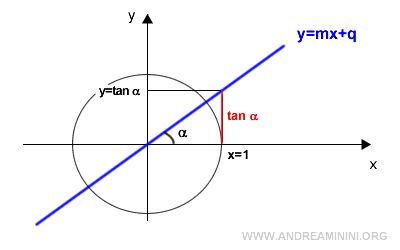
Demostración
Para simplificar, consideremos primero una recta que pasa por el origen; en este caso q=0.
$$ y = mx + q \ \ \ \ \ \ con \ q=0 $$
$$ y = mx $$
Representamos esta recta en el plano cartesiano:
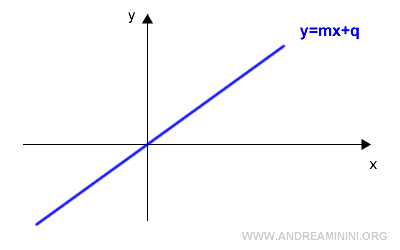
La pendiente m se expresa como:
$$ m = \frac{y}{x} $$
En la circunferencia unitaria el radio vale 1, por lo tanto x=1.
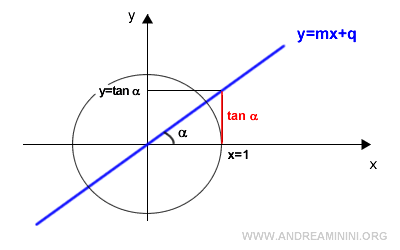
Al mismo tiempo, la coordenada y corresponde a la tangente del ángulo α, es decir: y = tan α.
El ángulo α es precisamente el que forma la recta con el eje x.
$$ m = \frac{y}{x} $$
$$ m = \frac{\tan \alpha}{1} $$
$$ m = \tan \alpha $$
En consecuencia, la pendiente de la recta es igual a la tangente del ángulo orientado que la recta forma con el eje x.
Nota: Este resultado sigue siendo válido aunque la recta no pase por el origen (q≠0). Todas las rectas paralelas determinan el mismo ángulo con el eje x. Como comparten el mismo ángulo α, también comparten el mismo valor de tangente, tan α. Por ello, todas las rectas paralelas tienen la misma pendiente m = tan α.
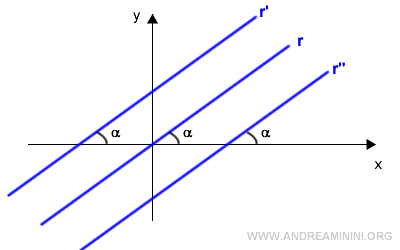
Y así sucesivamente.