Circunferencia unitaria
¿Qué es la circunferencia unitaria?
La circunferencia unitaria es aquella que tiene radio uno (r = 1), un punto inicial de referencia para los arcos (A) y sentido de recorrido antihorario, considerado positivo.
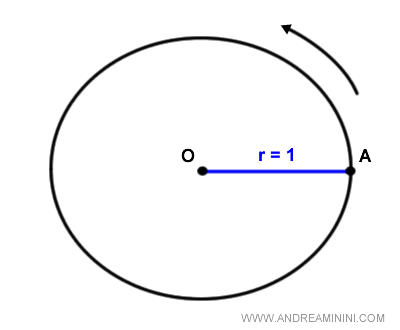
El punto A se encuentra en las coordenadas (x; y) = (1; 0) y se denomina punto inicial de los arcos.
La circunferencia unitaria se utiliza como base para medir ángulos.
Al escoger cualquier punto P sobre la circunferencia, se define un ángulo en el vértice O, limitado por los lados OA y OP.
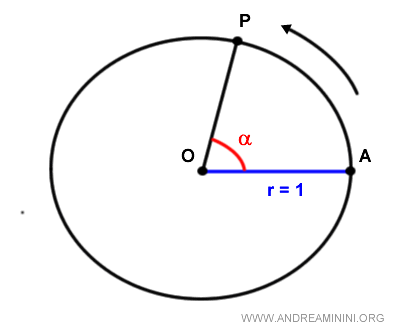
Dicho ángulo es un ángulo orientado, pues en la circunferencia unitaria se adopta, por convención, el sentido antihorario como positivo.
- El ángulo es positivo si se recorre la circunferencia en sentido antihorario.
- El ángulo es negativo si se recorre en sentido horario.
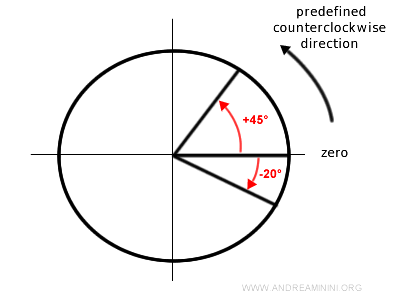
Nota: El centro de la circunferencia coincide con el origen O del sistema de coordenadas cartesianas, es decir, el punto (0, 0). En este sistema, el eje x positivo se toma como lado inicial de los ángulos orientados. Por tanto, el punto A, punto inicial de los arcos, se ubica en la coordenada (1, 0) del plano cartesiano.
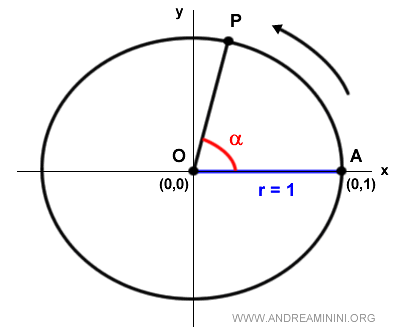
Dado que el radio es igual a uno (r = 1), la ecuación de la circunferencia unitaria en el plano cartesiano es $$ x^2 + y^2 = 1 $$
¿Cómo se mide la amplitud de un ángulo?
La amplitud de un ángulo suele expresarse en radianes (rad), salvo que se indique lo contrario.
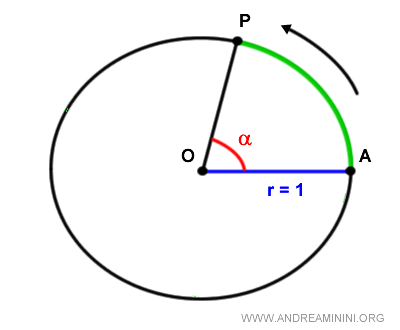
En radianes, la medida del ángulo se obtiene dividiendo la longitud del arco AP en la circunferencia unitaria entre el radio OA:
$$ \alpha = \frac{\overline{AP}}{\overline{OA}} \ rad $$
Así, en la circunferencia unitaria, un radián corresponde a un arco AP cuya longitud es exactamente igual al radio OA.
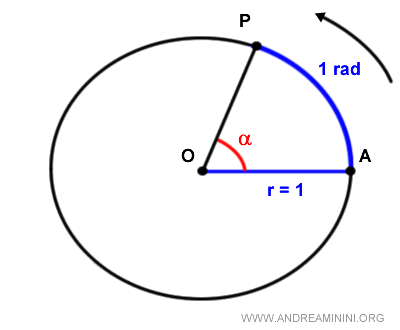
En este caso, como AP = OA, el cociente es igual a 1:
$$ \text{si} \ \overline{AP} = \ \overline{OA} \ \Rightarrow \ \frac{\overline{AP}}{\overline{OA}} = 1 \ rad $$
El radián (rad) es la unidad internacionalmente aceptada para expresar medidas angulares.
Nota: Existen otras unidades para medir ángulos, como los grados. No obstante, un ángulo solo debe expresarse en grados sexagesimales o grados decimales si así se especifica de forma explícita en el enunciado del problema.
¿Por qué medir los arcos en radianes?
La longitud de un arco de circunferencia en radianes se calcula mediante la siguiente fórmula:
$$ l = \alpha \cdot r $$
donde l es la longitud del arco, α es la medida del ángulo en radianes y r es el radio.
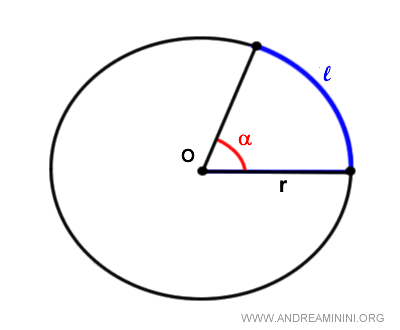
En la circunferencia unitaria, el radio tiene un valor de uno (r = 1).
$$ l = \alpha \cdot 1 $$
Por lo tanto, en la circunferencia unitaria, la longitud del arco en radianes coincide numéricamente con la medida del ángulo.
$$ l = \alpha $$
Esta es una de las ventajas fundamentales de emplear radianes (rad) para medir ángulos.
Y así sucesivamente.