Ángulos correspondientes
Se denominan ángulos correspondientes a los pares de ángulos que no comparten vértice y que ocupan la misma posición relativa respecto a dos rectas cortadas por una transversal.
En otras palabras, los ángulos correspondientes son aquellos que se sitúan en la misma «posición» dentro de la figura.
En cada par de ángulos correspondientes, uno es exterior y el otro es interior.
Un ejemplo práctico
Veamos un ejemplo práctico.
Consideremos dos rectas «r» y «s» cortadas por una transversal «t».
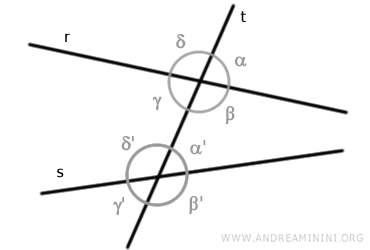
La intersección de la recta «t» con las otras dos genera ocho ángulos: α, β, γ, δ, α', β', γ', δ'
Los ángulos correspondientes forman pares de ángulos ubicados en la misma posición con respecto a la recta «t» y que no comparten vértice.
Por ejemplo, los ángulos α y α' constituyen un par de ángulos correspondientes.
El ángulo α se encuentra en la parte exterior respecto a las rectas, mientras que el ángulo α' está en la parte interior.
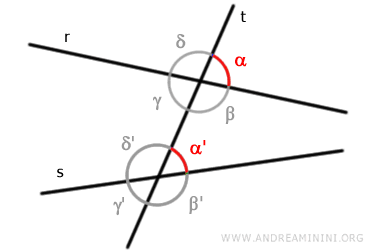
De manera similar, los ángulos β y β' son ángulos correspondientes.
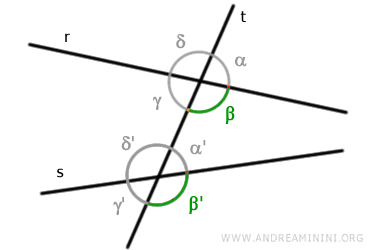
Asimismo, los ángulos γ y γ' forman otro par de ángulos correspondientes.
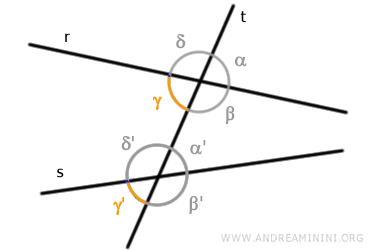
Por último, los ángulos δ y δ' completan el cuarto par de ángulos correspondientes.
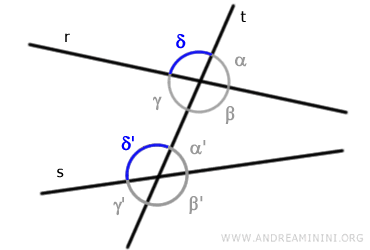
En todos estos casos, uno de los ángulos del par está situado en el interior, entre las rectas «r» y «s», mientras que el otro se encuentra en el exterior.
El caso de las rectas paralelas
Cuando las rectas «r» y «s» son paralelas y son cortadas por una transversal «t», los ángulos correspondientes resultan además congruentes, es decir, tienen exactamente la misma medida.
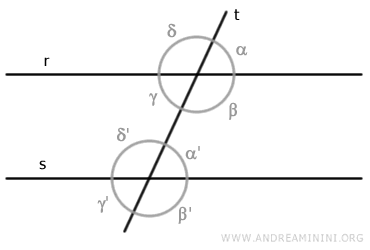
Por ejemplo, en este caso, los ángulos α y α' no solo son ángulos correspondientes, sino que también son congruentes, ya que miden lo mismo.
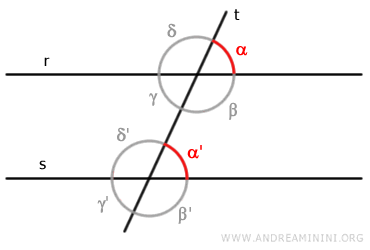
Esta es una de las propiedades fundamentales de las rectas paralelas en la geometría euclidiana y se emplea con frecuencia en demostraciones y teoremas geométricos.