Ángulos del mismo lado

Cuando dos rectas «r» y «s» son cortadas por una transversal «t», se denominan ángulos del mismo lado (o ángulos consecutivos) aquellos que no comparten vértice, que se encuentran ambos en el interior o ambos en el exterior de las rectas, y que están situados en el mismo lado de la transversal.

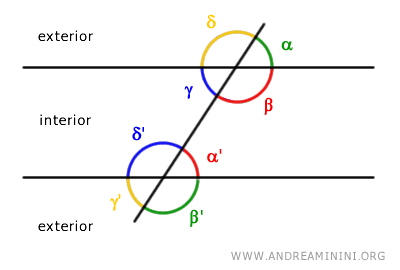
Los ángulos del mismo lado pueden clasificarse en:

• Ángulos interiores del mismo lado (o ángulos interiores consecutivos), cuando se ubican entre las rectas «r» y «s».
• Ángulos exteriores del mismo lado (o ángulos exteriores consecutivos), cuando se sitúan fuera del espacio comprendido entre las rectas.

Aquí tienes un ejemplo práctico:

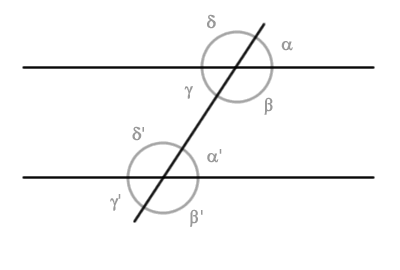
Consideremos dos rectas «r» y «s» cortadas por una transversal «t».

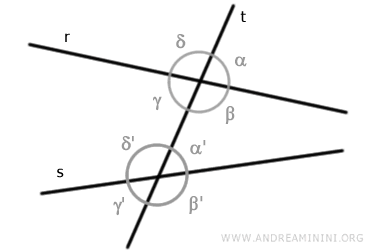
La intersección de estas rectas genera ocho ángulos.

Los pares de ángulos (β, α') y (γ, δ') se conocen como ángulos interiores del mismo lado.

Se denominan «interiores» porque están comprendidos en la zona entre las rectas «r» y «s».

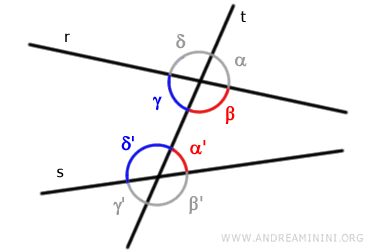
Por ejemplo, los ángulos rojos (β, α') no comparten vértice, son ambos interiores y se ubican en el mismo lado de la transversal. Lo mismo sucede con los ángulos azules (γ, δ').

Los pares de ángulos (α, β') y (δ, γ') se conocen como ángulos exteriores del mismo lado.

Se denominan «exteriores» porque se encuentran fuera del espacio delimitado por las rectas «r» y «s».

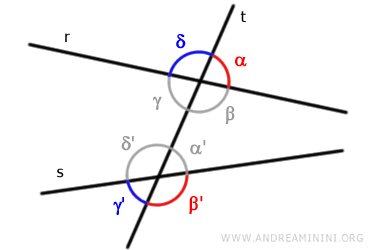
Por ejemplo, los ángulos exteriores rojos (α, β') no comparten vértice, son ambos exteriores y se sitúan en el mismo lado de la transversal. Lo mismo ocurre con los ángulos azules (δ, γ').

El caso de las rectas paralelas

Cuando las rectas «r» y «s» son paralelas, los ángulos del mismo lado también son ángulos suplementarios, ya que la suma de sus medidas es igual a un ángulo llano (180°).

Por ejemplo, los ángulos interiores del mismo lado (β, α') son, además, ángulos suplementarios.

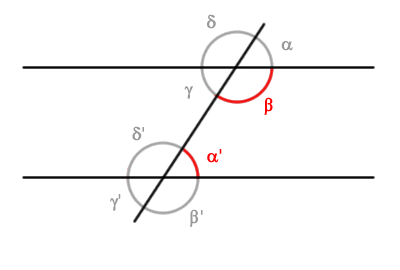
Esto se debe a que el ángulo α' es congruente con el ángulo α, es decir, ambos tienen la misma medida, y los ángulos α y β suman un ángulo llano (180°).

El mismo principio se aplica a los demás pares de ángulos del mismo lado: (α, β'), (δ, γ') y (γ, δ').