Ángulos Opuestos por el Vértice
Los ángulos opuestos por el vértice son dos ángulos que comparten el mismo vértice, cuyos lados se prolongan formando pares de rectas alineadas en direcciones opuestas.
En otras palabras, además de compartir el vértice, los lados de estos ángulos se sitúan sobre las mismas líneas rectas, extendiéndose en sentidos contrarios.
Un Ejemplo Práctico
Imaginemos que trazamos dos rectas que se cortan en un punto P.
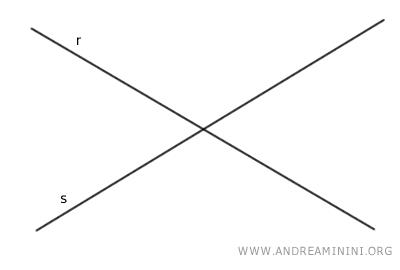
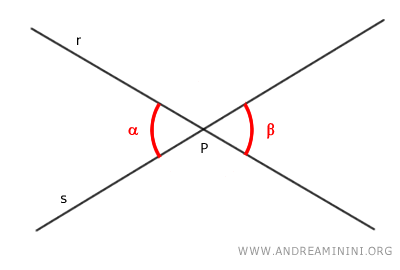
Estas rectas generan en el vértice P dos ángulos opuestos por el vértice, denominados alfa y beta.
Observaciones
Algunos aspectos clave sobre los ángulos opuestos por el vértice:
- Los ángulos opuestos por el vértice son siempre congruentes.
Demostración. Consideremos los ángulos opuestos por el vértice alfa y beta, junto con otro ángulo gamma.
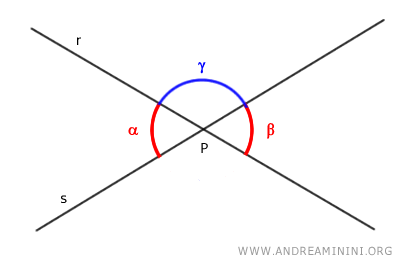
La suma de los ángulos alfa y gamma es 180°, formando un ángulo llano. Por tanto, alfa y gamma son ángulos adyacentes. $$ \alpha + \gamma = 180° $$ De manera análoga, los ángulos beta y gamma también son adyacentes, ya que su suma es igualmente 180°. $$ \beta + \gamma = 180° $$ Resolviendo este sistema de ecuaciones para alfa y beta, se demuestra que ambos ángulos son congruentes: $$ \alpha = 180° - \gamma $$ $$ \beta = 180° - \gamma $$ - Ángulos Exteriores
En un polígono, dos ángulos exteriores (βe y β'e) situados en el mismo vértice (B) son opuestos por el vértice y, por tanto, congruentes: βe≅β'e. Cada uno de estos ángulos exteriores es suplementario de su ángulo interior correspondiente (β), es decir, βe + β = 180° y β'e + β = 180°. Por esta razón, suele hablarse simplemente de "ángulo exterior" sin necesidad de diferenciar entre uno u otro.

Y así sucesivamente.