Cómo medir el arco de una circunferencia
Para calcular la longitud de un arco de circunferencia (l), basta con multiplicar el ángulo en radianes (α) por el radio de la circunferencia (r). $$ l = \alpha \cdot r $$
Ejemplo
Veamos cómo calcular la longitud de un arco de circunferencia (l).
El ángulo es de π/3 (equivalente a 60°) y el radio de la circunferencia es r = 5 cm.
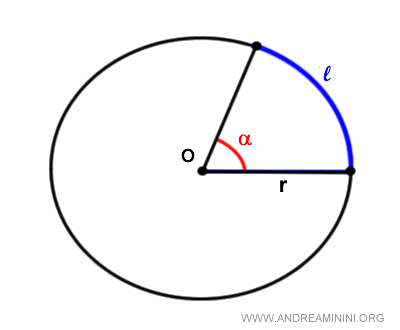
La longitud del arco es de 5,23 cm.
$$ l = \alpha \cdot r $$ $$ l = \frac{\pi}{3} \cdot 5 \ cm $$ $$ l = \frac{3,14 \cdot 5}{3} \ cm $$ $$ l = 5,23 \ cm $$
Nota: Es fundamental que el ángulo esté expresado en radianes. Si el ángulo se encuentra en grados (por ejemplo, 60°), es necesario convertirlo previamente a radianes antes de aplicar la fórmula.
Demostración
La demostración es muy sencilla.
Un ángulo medido en radianes se define como el cociente entre la longitud del arco (l) y el radio de la circunferencia (r):
$$ \alpha = \frac{ l }{ r } $$
Con una simple transformación algebraica, se obtiene la longitud del arco en función del radio y del ángulo:
$$ l = \alpha \cdot r $$
Esto pone de manifiesto una de las grandes ventajas de utilizar radianes para medir ángulos.
Y así sucesivamente.