Ángulos

Un ángulo es la región del plano comprendida entre dos semirrectas que comparten un mismo punto de origen.

A estas dos semirrectas se las denomina lados del ángulo.

El punto común de inicio se llama el vértice del ángulo.

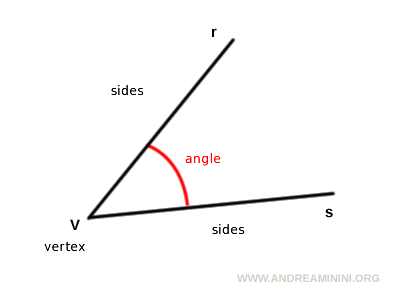
La medida de un ángulo entre sus dos lados puede expresarse en grados, usando el sistema sexagesimal, o en radianes.

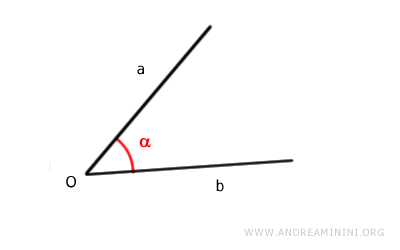
Para representar la medida de un ángulo, se suele emplear una letra griega minúscula (por ejemplo, α, β, γ, etc.).

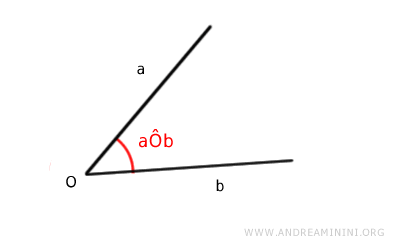
Otra notación posible es aÔb, donde “a” y “b” representan los lados, y “Ô” es el vértice del ángulo.

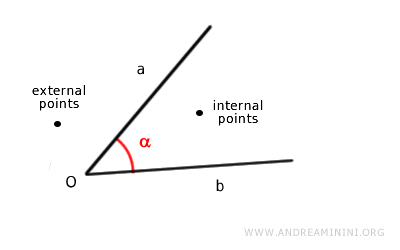
Todos los puntos situados entre los lados del ángulo y que no se encuentran sobre las semirrectas se llaman puntos interiores del ángulo.

El resto de los puntos se denominan puntos exteriores al ángulo.

Medición de ángulos

Para establecer la medida de un ángulo, se le asigna un valor numérico de acuerdo con un sistema de medición.

Los principales sistemas para medir ángulos son el de grados (sexagesimal) y el de radianes.

• Medición en grados
  Este sistema divide la circunferencia (ángulo completo) en 360 partes iguales llamadas grados.
• Medición en radianes
  Un radián es el ángulo que abarca un arco cuya longitud es igual al radio de la circunferencia. En una vuelta completa hay 2π radianes, lo que equivale aproximadamente a 6,28 radianes.

Medir ángulos nos permite clasificar todos los ángulos del plano en conjuntos o clases de ángulos congruentes.

Cada clase agrupa todos los ángulos que tienen la misma medida.

En particular, dos o más ángulos se consideran congruentes si tienen la misma amplitud.

Por tanto, los ángulos congruentes pertenecen a la misma clase de equivalencia.

Nota: Los ángulos congruentes no necesariamente comparten los mismos puntos en el plano ni la misma orientación en el espacio. Lo que importa en la relación de congruencia es que midan lo mismo.

Para comparar dos ángulos, se superpone el primero sobre el segundo mediante un movimiento rígido, de modo que uno de sus lados coincida y ambos queden en el mismo lado de la recta común.

Si los ángulos coinciden perfectamente, entonces son congruentes $ \alpha \cong \beta $. En caso contrario, tienen medidas diferentes.

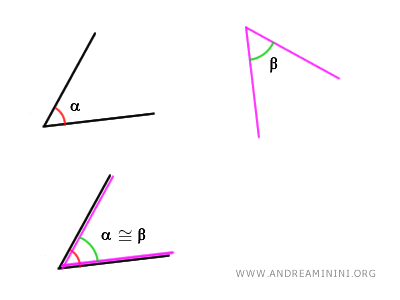
La longitud de los lados no influye, ya que el tamaño de un ángulo no depende de la longitud de sus lados, sino de la apertura que forman.

Tipos de ángulos

Existen distintos tipos de ángulos.

• Ángulos cóncavos
  Un ángulo es cóncavo si contiene las prolongaciones de sus lados.
  
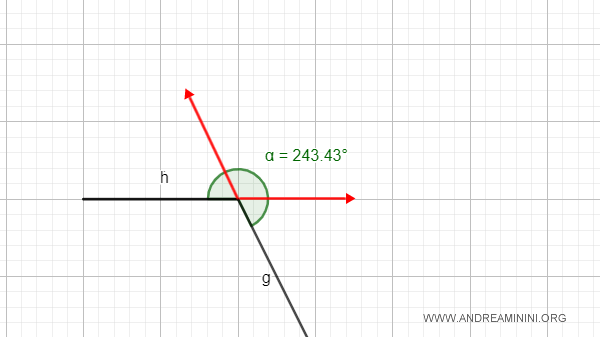
• Ángulos convexos
  Un ángulo es convexo si no contiene las prolongaciones de sus lados.
  
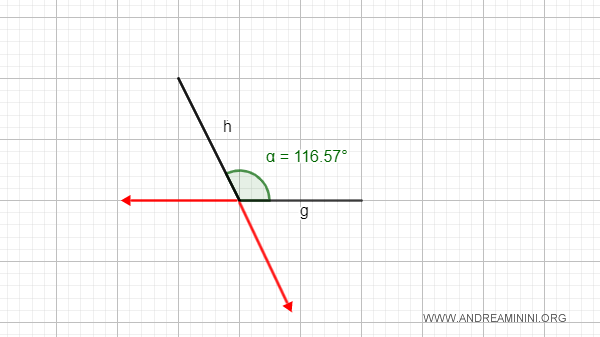
• Ángulo recto
  Un ángulo recto se forma cuando las rectas son perpendiculares, creando cuatro ángulos iguales entre sí. Su medida es de 90° (π/2 radianes).
  

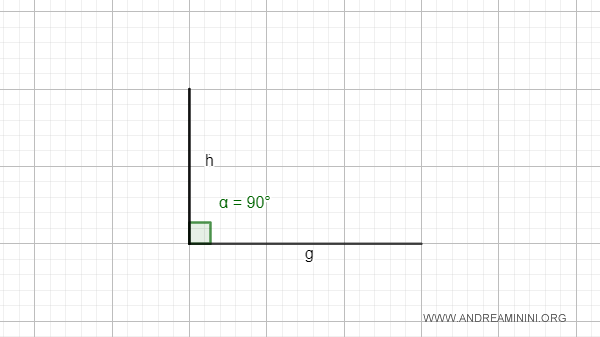
  Nota: Dos ángulos son congruentes cuando tienen la misma medida.

• Ángulo completo
  Un ángulo completo se da cuando los lados coinciden, abarcando todos los puntos del plano. Su medida es de 360° (2π radianes).
  

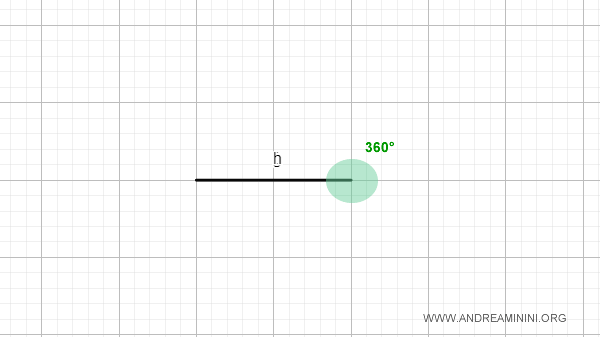
  Nota: En un ángulo completo, los lados son semirrectas coincidentes.

• Ángulo nulo
  Un ángulo nulo se produce cuando los lados coinciden y el ángulo solo contiene los puntos sobre esas semirrectas. Su medida es de 0° (cero radianes).

Ángulos orientados

Por convención, un ángulo es positivo cuando la rotación se realiza en sentido antihorario.

El lado inicial asociado al ángulo nulo corresponde al eje x positivo.

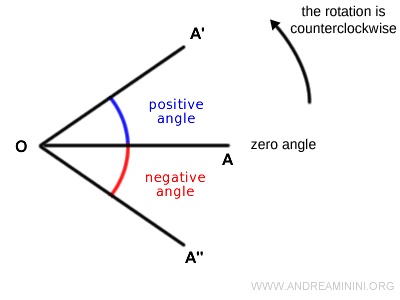
Por el contrario, si la rotación es en sentido horario, el ángulo se considera negativo.

Esta convención se emplea prácticamente en todos los textos de matemáticas y física.

Ángulos adyacentes y consecutivos

Los ángulos adyacentes y los consecutivos se diferencian por cómo se sitúan respecto a una recta o un punto.

• Ángulos consecutivos
  Dos ángulos son consecutivos si comparten un vértice y uno de sus lados.
  
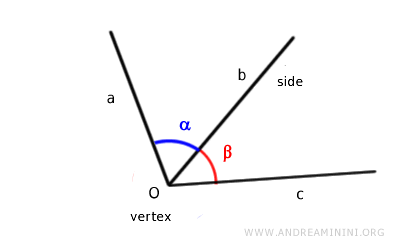
• Ángulos adyacentes
  Dos ángulos son adyacentes si comparten un vértice y un lado, y sus lados no comunes se encuentran sobre la misma recta.
  

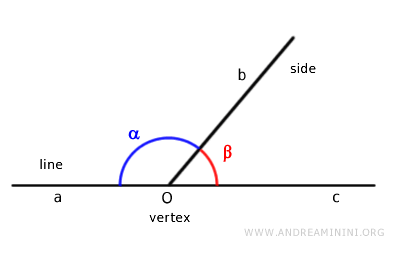
  Nota: Los ángulos adyacentes son también consecutivos, pero no siempre ocurre lo contrario. La suma de dos ángulos adyacentes siempre es 180°, lo que corresponde a un ángulo llano.

Ángulos cóncavos y convexos

Los ángulos pueden clasificarse como cóncavos o convexos.

• Ángulos cóncavos
  Un ángulo se define como cóncavo cuando incluye las prolongaciones de sus lados, salvo en el caso del ángulo completo.
  
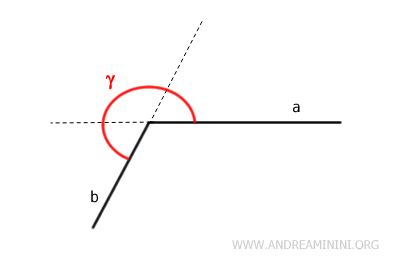
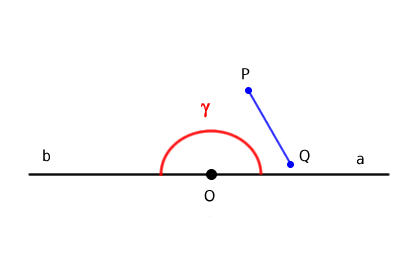
  Otra forma de identificar un ángulo cóncavo es eligiendo dos puntos interiores, P y Q, y trazando un segmento que los una. Si este segmento no queda completamente dentro del ángulo, es decir, si atraviesa puntos exteriores, el ángulo es cóncavo.
  

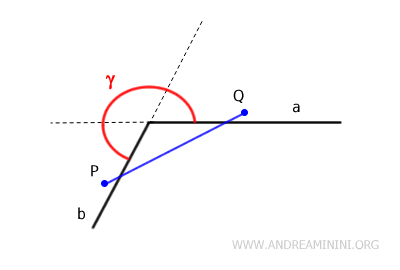
  Nota: Un ángulo completo (360 grados) no se considera cóncavo, porque cualquier par de puntos interiores puede unirse mediante un segmento contenido íntegramente en el ángulo, sin atravesar puntos exteriores.

• Ángulos convexos
  Un ángulo se considera convexo si no incluye las prolongaciones de sus lados.
  
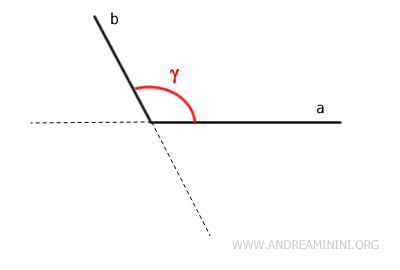
  En este caso, si se eligen dos puntos P y Q dentro del ángulo y se unen con un segmento, dicho segmento permanece completamente dentro del ángulo, es decir, no atraviesa ningún punto exterior.
  
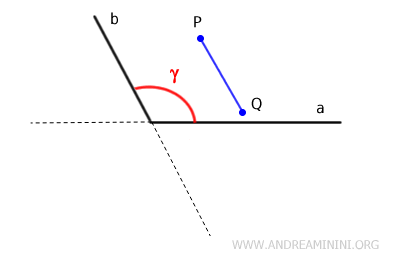
  Por tanto, todos los ángulos comprendidos entre 0 y 180° se consideran convexos.
  

  Nota: Un ángulo llano (180°) se considera convexo porque los puntos situados sobre sus lados no se consideran puntos interiores. Así, cualquier segmento que una dos puntos interiores no intersecta los lados ni sus prolongaciones.
  

Y así sucesivamente