Ángulos Asociados en Geometría

En geometría, se denominan "ángulos asociados" a aquellos que están vinculados entre sí por una relación específica.

Los ángulos pueden estar asociados por su medida, por su posición o por la forma en que se relacionan respecto a dos rectas que se cortan.

Ángulos Asociados por su Medida

Se dice que dos ángulos están asociados por su medida cuando la suma de sus amplitudes equivale a un ángulo recto o a un múltiplo de este.

En particular, los ángulos asociados por medida se clasifican en:

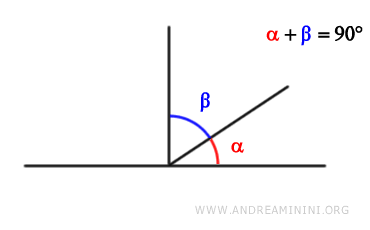
• Ángulos Complementarios
  Dos ángulos son complementarios si la suma de sus medidas es un ángulo recto (90° o π/2 radianes).
  
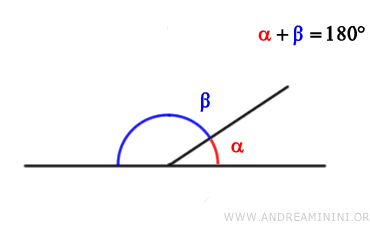
• Ángulos Suplementarios
  Dos ángulos son suplementarios si la suma de sus medidas forma un ángulo llano (180° o π radianes).
  
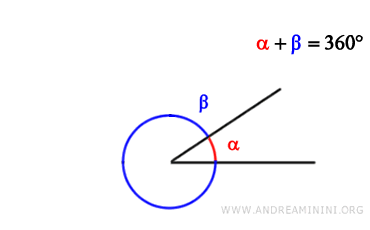
• Ángulos Explementarios
  Dos ángulos se consideran explementarios si la suma de sus medidas equivale a un ángulo completo (360° o 2π radianes).
  

Ángulos Asociados por su Posición

Dos ángulos están asociados por su posición cuando comparten uno o más lados, o bien las prolongaciones de estos.

Podemos distinguir varios tipos de ángulos asociados por posición:

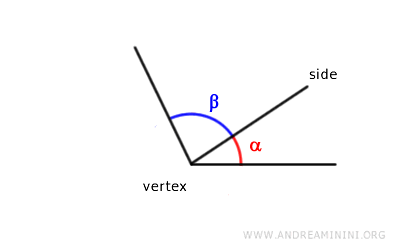
• Ángulos Consecutivos
  Dos ángulos son consecutivos si tienen el mismo vértice y comparten uno de sus lados.
  
• Ángulos Adyacentes
  Dos ángulos son adyacentes cuando tienen el mismo vértice y un lado común, y los lados no comunes se encuentran sobre la misma recta.
  

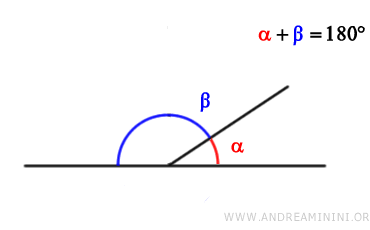
  Nota: Es decir, los ángulos adyacentes son un caso particular de ángulos consecutivos, en los que los lados no comunes se sitúan sobre una misma línea recta. Además, los ángulos adyacentes siempre son suplementarios, ya que su suma equivale a un ángulo llano (180°).

• Ángulos Opuestos por el Vértice
  Dos ángulos son opuestos por el vértice si no son consecutivos, comparten el mismo vértice y los lados de uno son prolongaciones de los lados del otro.
  
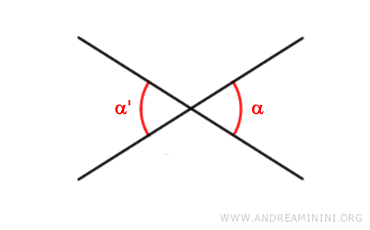
  Por ejemplo, los ángulos α y α' son ángulos opuestos por el vértice.
  

  Nota: Los ángulos opuestos por el vértice siempre son congruentes, ya que tienen exactamente la misma medida.

Ángulos Asociados respecto a Dos Rectas que se Cortan

Consideremos dos rectas "r" y "s" que son intersectadas por una recta transversal "t", formando ocho ángulos que mantienen entre sí ciertas relaciones específicas.

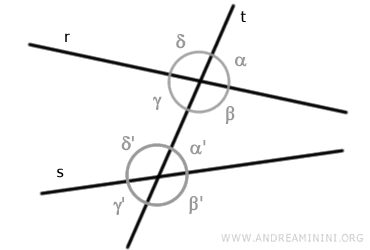
Las relaciones entre estos ángulos asociados son las siguientes:

• Ángulos Alternos
  Se trata de pares de ángulos que no comparten vértice y se encuentran a lados opuestos de la recta transversal "t".
  

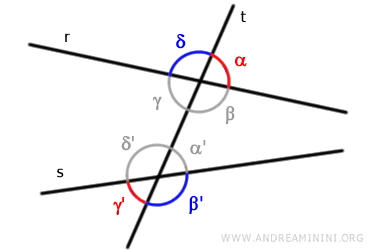
  Pueden ser alternos internos o alternos externos, según se sitúen entre las rectas "r" y "s" o fuera de ellas. Por ejemplo, los pares de ángulos (γ, α') y (β, δ') son alternos internos.
  
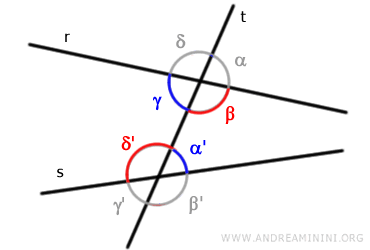
  Los pares de ángulos (α, γ') y (δ, β') se consideran alternos externos.
  

• Ángulos Conjugados
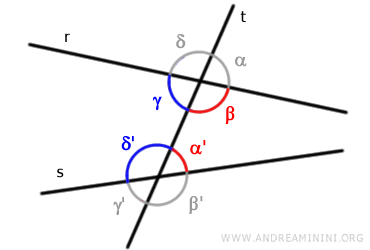
  Son pares de ángulos del mismo lado que no comparten vértice y se encuentran en el mismo lado de la recta transversal "t".
  

  Se les conoce también como colaterales internos o colaterales externos, según estén comprendidos entre las rectas "r" y "s" o fuera de ellas. Por ejemplo, los pares de ángulos (β, α') y (γ, δ') son colaterales internos.
  
  Por el contrario, los pares de ángulos (α, β') y (δ, γ') son colaterales externos.
  
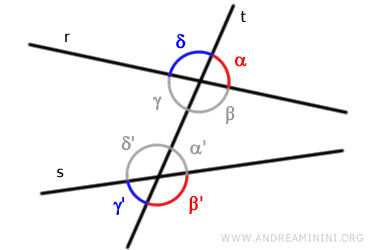
  Cuando las rectas "r" y "s" son paralelas, los ángulos colaterales internos también resultan suplementarios, pues suman un ángulo llano (180°).

• Ángulos Correspondientes
  Son pares de ángulos que no comparten vértice, se sitúan en el mismo lado de la transversal "t" y uno queda en el interior y otro en el exterior respecto a las dos rectas.
  

  Por ejemplo, los pares de ángulos (α, α'), (β, β'), (γ, γ') y (δ, δ') se denominan ángulos correspondientes.
  
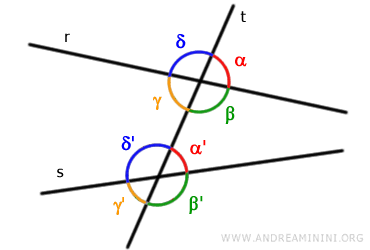
  Los ángulos correspondientes son congruentes únicamente si las rectas "r" y "s" son paralelas.

Ángulos Asociados en Trigonometría

En trigonometría, se habla de "ángulos asociados" para referirse a pares de ángulos que mantienen entre sí relaciones definidas por las funciones trigonométricas.

Algunas de las principales relaciones trigonométricas son:

$$ \sin (- \alpha) = - \sin (\alpha) $$

$$ \sin \left( \frac{\pi}{2} - \alpha \right) = \cos (\alpha) $$

$$ \sin \left( \frac{\pi}{2} + \alpha \right) = \cos (\alpha) $$

$$ \sin (\pi - \alpha) = \sin (\alpha) $$

$$ \cos (- \alpha) = \cos (\alpha) $$

$$ \cos \left( \frac{\pi}{2} - \alpha \right ) = \sin (\alpha) $$

$$ \cos \left( \frac{\pi}{2} + \alpha \right) = - \sin (\alpha) $$

$$ \cos (\pi - \alpha) = - \cos (\alpha) $$

$$ \tan (- \alpha) = - \tan (\alpha) $$

$$ \tan \left( \frac{\pi}{2} - \alpha \right) = \cot (\alpha) $$

$$ \tan \left( \frac{\pi}{2} + \alpha \right) = - \cot (\alpha) $$

$$ \tan (\pi - \alpha) = - \tan (\alpha) $$

Y así sucesivamente.