Ángulos Complementarios
Se llaman ángulos complementarios a dos ángulos cuya suma es igual a 90° o π/2 radianes.
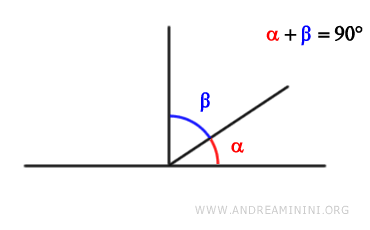
La palabra «complementario» proviene del latín «complementum», que significa «lo que completa».
En este contexto, un ángulo completa al otro para formar un ángulo recto de 90 grados.
Nota: No importa cuánto mida cada ángulo por separado, siempre que la suma de ambos sea 90°.
Un Ejemplo Práctico
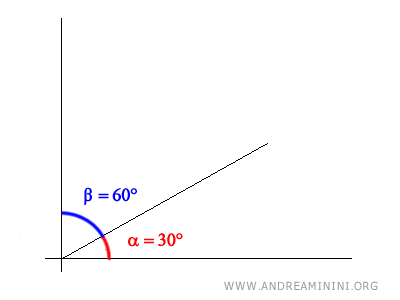
Por ejemplo, observemos dos ángulos, alfa y beta:
$$ \alpha = 30° $$
$$ \beta = 60° $$
Estos ángulos son complementarios porque al sumarlos se obtiene 90°.
$$ \alpha + \beta = 30° + 60° = 90° $$
De forma gráfica:
Todo ángulo tiene su ángulo complementario.
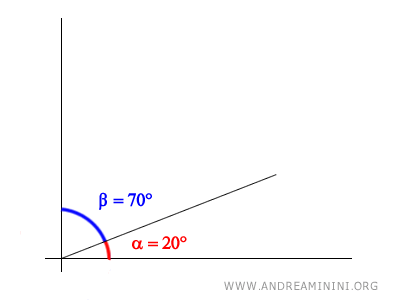
Por ejemplo, considera el siguiente ángulo:
$$ \alpha = 20° $$
Para encontrar su ángulo complementario, basta restar su medida a 90°.
$$ \beta = 90° - \alpha $$
$$ \beta = 90° - 20° $$
$$ \beta = 70° $$
En este caso, el ángulo complementario es de 70°.
Observaciones
Algunas propiedades y observaciones sobre los ángulos complementarios:
- Si dos ángulos, α y β, son complementarios de un mismo ángulo γ, entonces α y β son congruentes. $$ \alpha + \gamma = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \beta $$
Demostración: Dado que la suma de los ángulos es constante (90 grados), si uno de ellos se mantiene fijo, el otro debe tener el mismo valor en ambos pares. Sabemos que $$ \alpha + \gamma = 90° $$ y $$ \beta + \gamma = 90° $$. Si despejamos γ de la segunda ecuación: $$ \gamma = 90° - \beta $$ y sustituimos en la primera, obtenemos: $$ \alpha + ( 90° - \beta ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \beta = \cancel{90°} $$ $$ \alpha - \beta = 0° $$ Lo que implica que α y β tienen la misma medida. Por tanto, α y β son congruentes. $$ \alpha \cong \beta $$
- Si un ángulo es complementario de un segundo ángulo, y ese segundo ángulo es complementario de un tercero, entonces el primero y el tercero son iguales. $$ \alpha + \beta = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \gamma $$
Demostración: Sabemos que $$ \alpha + \beta = 90° $$ y $$ \beta + \gamma = 90° $$. Despejamos β de la segunda ecuación: $$ \beta = 90° - \gamma $$ y lo sustituimos en la primera: $$ \alpha + ( 90° - \gamma ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \gamma = \cancel{90°} $$ $$ \alpha - \gamma = 0° $$ Esto indica que α y γ miden lo mismo, es decir, son ángulos congruentes. $$ \alpha \cong \gamma $$
- Si dos ángulos, α y β, son complementarios del mismo ángulo γ, entonces α y β son congruentes, es decir, tienen la misma medida.
Demostración: Consideremos dos pares de ángulos complementarios: $$ \alpha + \gamma = 90° $$ $$ \beta + \gamma = 90° $$. Hallamos α y β restando γ a 90 grados: $$ \alpha = 90° - \gamma $$ $$ \beta = 90° - \gamma $$ Esto demuestra que α y β tienen la misma medida: $$ \alpha = \beta = 90° - \gamma $$ Por tanto, α y β son congruentes.
- Dos ángulos complementarios, α y β, asociados a dos ángulos congruentes, γ₁ y γ₂, también resultan ser congruentes entre sí: $$ \alpha \cong \beta $$.
Demostración: Por definición, los ángulos complementarios suman un ángulo recto. Por tanto: $$ \alpha + \gamma_1 = 90^\circ $$ $$ \alpha + \gamma_2 = 90^\circ $$ Como γ₁ y γ₂ son congruentes: $$ \gamma_1 \cong \gamma_2 $$ podemos expresar α y β de la siguiente manera: $$ \alpha = 90^\circ - \gamma_1 $$ $$ \beta = 90^\circ - \gamma_2 $$ Dado que $$ \gamma_1 \cong \gamma_2 $$ se deduce que: $$ \alpha = 90^\circ - \gamma_1 $$ $$ \beta = 90^\circ - \gamma_1 $$ Por tanto, α y β son congruentes: $$ \alpha \cong \beta \cong 90^\circ - \gamma_1 $$
- El seno de un ángulo es igual al coseno de su ángulo complementario. $$ \alpha + \beta = 90° \Longrightarrow \sin( \alpha ) = \cos( \beta ) $$
Por ejemplo, los ángulos de 70° y 20° son complementarios porque suman un ángulo recto: $$ 70° + 20° = 90° $$. El coseno de 70° es igual al seno de 20°: $$ \cos(70°) = \sin(20°) = 0.94 $$. Esto ocurre porque en trigonometría existe una relación fundamental entre ángulos complementarios. Las funciones trigonométricas de ángulos complementarios están íntimamente relacionadas.
Demostración: Consideremos la circunferencia unitaria y un ángulo α que forma el triángulo rectángulo OAB.
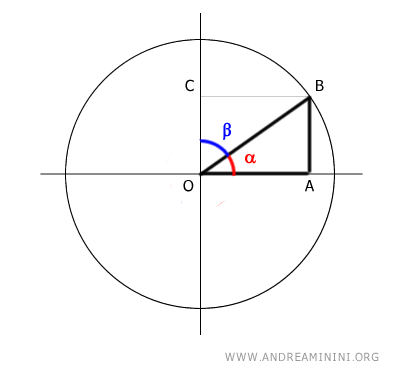
El seno del ángulo α es la razón entre el cateto opuesto (AB) y la hipotenusa (OB): $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } $$ Mientras que el coseno de α es la razón entre el cateto adyacente (OA) y la hipotenusa (OB): $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } $$. El ángulo complementario de α es β: $$ \alpha + \beta = 90° $$. Como los segmentos OA y CB son congruentes: $$ \overline{OA} \cong \overline{CB} $$ también podemos expresar el coseno mediante la razón CB/OB: $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } $$. Si analizamos el triángulo OBC (el triángulo morado), el segmento CB es el cateto opuesto al ángulo β.
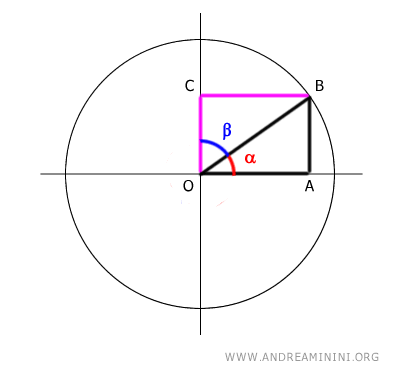
Por tanto, la razón CB/OB corresponde al seno de β: $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } = \sin \beta $$. En consecuencia, el coseno de α es igual al seno de su ángulo complementario β: $$ \cos \alpha = \sin \beta $$. Además, sabiendo que los segmentos AB y OC son congruentes: $$ \overline{AB} = \overline{OC} $$ y siguiendo un razonamiento similar: $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } = \frac{ \overline{OC} }{ \overline{OB} } = \cos \beta $$ se concluye que el seno de α es igual al coseno de su ángulo complementario β: $$ \sin \alpha = \cos \beta $$. Esto es lo que queríamos demostrar.
Los ángulos complementarios son un concepto fundamental en geometría y poseen múltiples aplicaciones prácticas.
Por ejemplo, se utilizan en el diseño y construcción de edificaciones y estructuras, donde los ángulos rectos son muy frecuentes. También tienen relevancia en navegación, cartografía y en numerosas disciplinas científicas.
Y así sucesivamente.