Postulado de Eudoxo-Arquímedes sobre Ángulos
El postulado de Eudoxo-Arquímedes afirma que, dados dos ángulos no congruentes y de medida distinta de cero, siempre es posible encontrar un múltiplo del ángulo menor que exceda la medida del ángulo mayor.
Este principio es fundamental en la geometría euclidiana.
El postulado recibe su nombre de los matemáticos de la antigüedad Eudoxo y Arquímedes, quienes lo formularon y emplearon en sus estudios.
Nota: Este postulado aplica, al caso de los ángulos, el conocido postulado de Eudoxo-Arquímedes sobre segmentos.
Un Ejemplo Práctico
Consideremos dos ángulos, alfa y beta.
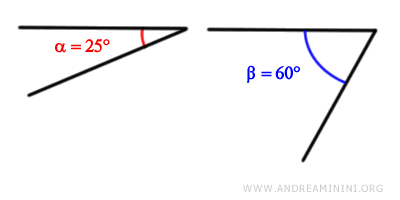
Ambos ángulos tienen medidas mayores que cero.
$$ \alpha = 25° $$
$$ \beta = 60° $$
Además, estos dos ángulos no son congruentes, ya que el ángulo beta posee una medida superior a la del ángulo alfa.
En este caso, existe un múltiplo del ángulo menor (alfa) que supera la medida del ángulo mayor (beta).
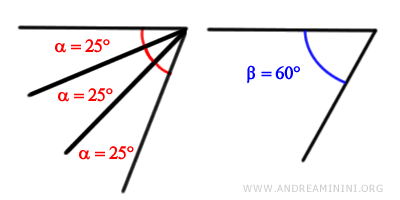
Dicho múltiplo es 3 veces el ángulo alfa:
$$ 3 \cdot \alpha > \beta $$
$$ 3 \cdot 25° > 60° $$
$$ 75° > 60° $$
Por tanto, sea cual sea la medida de dos ángulos no congruentes, siempre que sean distintos de cero, es posible hallar un múltiplo del ángulo menor que supere la medida del ángulo mayor.
Y así sucesivamente.