Postulado de Eudoxo-Arquímedes sobre Segmentos
El Postulado de Eudoxo-Arquímedes establece que, dados dos segmentos de longitudes distintas (no congruentes) y diferentes de cero, siempre es posible encontrar un múltiplo del segmento más corto que supere la longitud del segmento más largo.
Este principio también es conocido como el principio arquimediano, ya que Arquímedes lo utilizó en numerosas demostraciones geométricas.
En esencia, el postulado afirma que siempre se puede “escalar” un segmento más corto hasta superar la longitud de otro más largo, multiplicándolo un número finito de veces.
Nota: Este es un concepto fundamental en matemáticas, especialmente en geometría y en análisis matemático. El principio arquimediano sustenta muchos campos de las matemáticas, entre ellos la construcción de los números reales y el concepto de límite, esencial en cálculo.
Un Ejemplo Práctico
Consideremos dos segmentos, AB y CD.
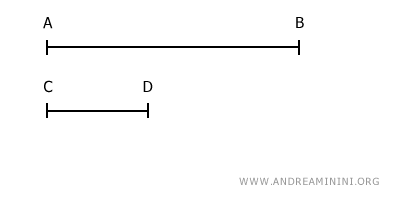
Ambos segmentos tienen longitud positiva (distinta de cero) y son diferentes entre sí, es decir, no son congruentes.
El segmento AB es más largo que el segmento CD.
Multiplicamos el segmento más corto, CD, por dos.
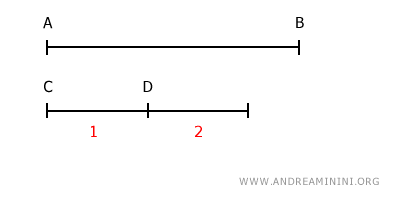
El segmento resultante sigue siendo más corto que AB.
Probemos entonces multiplicar el segmento CD por tres.
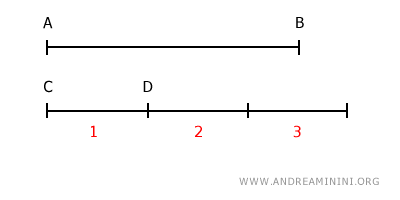
En este caso, el segmento resultante excede la longitud del segmento AB.
Por lo tanto, el segmento que mide tres veces la longitud del segmento más corto CD supera la longitud del segmento más largo AB.
Y así sucesivamente.