Múltiplos y Submúltiplos de Segmentos

En geometría, los conceptos de múltiplos y submúltiplos de un segmento se utilizan de manera similar a como se emplean en matemáticas para los números.

• Múltiplo de un Segmento
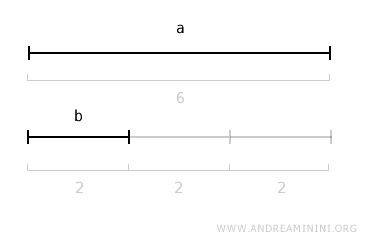
  Se dice que un segmento es múltiplo de otro cuando su longitud es igual a la del segmento original multiplicada por un número natural (N>1).

  Ejemplo. Supongamos que tengo un segmento “a” de 6 unidades de longitud y un segmento “b” de 2 unidades. En este caso, el segmento “a” es múltiplo del segmento “b”, ya que equivale a “b” multiplicado por N=3, o bien a la suma de N=3 segmentos iguales en longitud a “b”.
  

• Submúltiplo de un Segmento
  Se dice que un segmento es submúltiplo de otro cuando su longitud es igual a la del segmento original dividida entre un número natural (N>1).
  

  Ejemplo. Supongamos que tengo un segmento “a” de 6 unidades y un segmento “b” de 2 unidades. En este caso, el segmento “b” es submúltiplo del segmento “a”, ya que equivale a “a” dividido entre N=3.
  
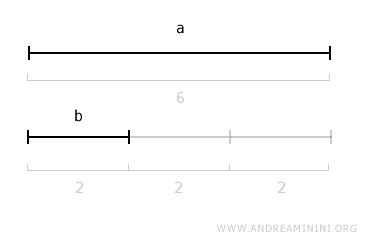
  En términos prácticos, el segmento “b” es submúltiplo de “a” porque su longitud representa 1/3 de la longitud del segmento “a”: $$ b = \frac{1}{3} \cdot a $$

Estos conceptos son muy útiles en geometría para describir las relaciones entre las longitudes de distintos segmentos dentro de un dibujo o figura.

Y así sucesivamente.