Segmentos Conmensurables e Inconmensurables
Dos segmentos se consideran conmensurables si la razón entre sus longitudes es un número racional \( \frac{a}{b} \). En caso contrario, se dice que son inconmensurables.
Si dos segmentos son conmensurables, es posible dividirlos exactamente en un mismo número de partes iguales, utilizando un segmento común como unidad de medida.
Segmentos Conmensurables
Decimos que dos segmentos son conmensurables si existe una unidad común de medida (un segmento de referencia) tal que las longitudes de ambos puedan expresarse como múltiplos enteros de esa unidad.
En términos sencillos, esto significa que la razón entre sus longitudes es un número racional \( \frac{a}{b} \), donde \( a \) y \( b \) son enteros.
Ejemplo
Consideremos dos segmentos que miden \(3\) cm y \(4\) cm, respectivamente.
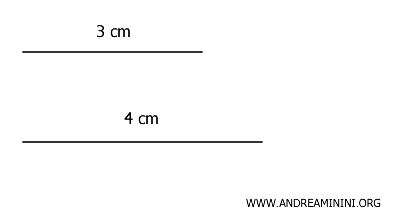
Como la razón entre sus longitudes es \(3/4\), que es un número racional, estos segmentos son conmensurables.
Esto implica que podemos dividir ambos segmentos en un número exacto de partes iguales, utilizando un mismo segmento como unidad de medida.
Para determinar esa unidad común, calculamos el máximo común divisor (MCD) de sus longitudes.
$$ MCD(3, 4) = 1 $$
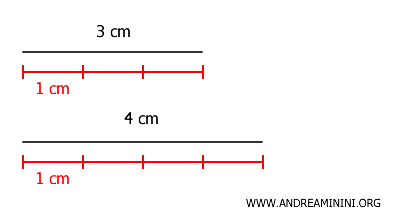
En este caso, el máximo común divisor es 1, lo que indica que los segmentos de 3 cm y 4 cm pueden dividirse en segmentos de 1 cm de longitud.
Al dividir ambos en unidades de 1 cm, sus longitudes se expresan respectivamente como \(3\) y \(4\) unidades.
Segmentos Inconmensurables
Dos segmentos se consideran inconmensurables si no existe ninguna unidad común de medida que permita expresar sus longitudes como múltiplos enteros.
Esto sucede cuando la razón entre sus longitudes es un número irracional, es decir, un número que no puede expresarse como una fracción.
Ejemplo
Un ejemplo clásico en geometría es el del lado y la diagonal de un cuadrado.
Si el lado del cuadrado mide \(1\) cm, según el teorema de Pitágoras, su diagonal mide \( \sqrt{2} \) cm.
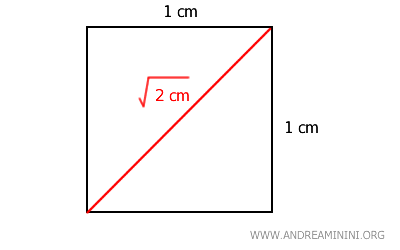
La razón entre el lado del cuadrado (\(1\)) y su diagonal (\( \sqrt{2} \)) no puede expresarse como un número racional \( \frac{a}{b} \), donde \( a \) y \( b \) sean enteros, pues \( \sqrt{2} \) es irracional.
Por ello, estos dos segmentos son inconmensurables.
Nota: Este hallazgo supuso un gran desafío para la escuela pitagórica, ya que contradecía su creencia de que toda relación podía expresarse mediante números racionales. El descubrimiento marcó un punto de inflexión en la historia de las matemáticas, dando lugar al concepto de número irracional. Según la tradición, los pitagóricos procuraron mantener en secreto el descubrimiento de los irracionales, temiendo que amenazara su visión del mundo basada en la armonía y racionalidad numérica. La leyenda cuenta que el discípulo que reveló esta verdad, Hipaso de Metaponto, fue severamente castigado por los pitagóricos; algunas versiones incluso sostienen que fue condenado a muerte o arrojado al mar.
Y así sucesivamente.