Segmentos de recta
Un segmento es una porción de una recta delimitada por dos puntos, A y B, denominados extremos.

Los extremos A y B determinan los límites del segmento y pertenecen a él.
Así pues, el segmento se representa como un tramo de línea recta que va de un punto al otro.
Todos los puntos comprendidos entre los extremos se denominan puntos interiores del segmento.
Nota. Aunque el segmento es un tramo limitado de recta, está formado por infinitos puntos, ya que entre dos puntos cualesquiera del segmento siempre es posible encontrar otro punto intermedio. En otras palabras, el segmento es un conjunto denso. Existe una excepción: el segmento nulo. Cuando ambos extremos coinciden, se obtiene un segmento nulo, compuesto únicamente por un punto.
Un segmento puede considerarse parte de una recta.
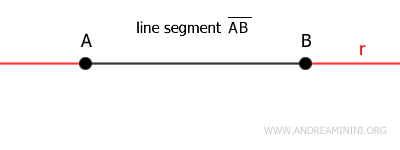
Las semirrectas que pertenecen a la misma recta "r" y parten de uno de los extremos del segmento, prolongándose sin alcanzar el otro, se denominan prolongaciones del segmento.
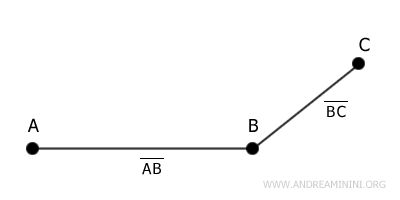
Se dice que dos segmentos son consecutivos si comparten un extremo.
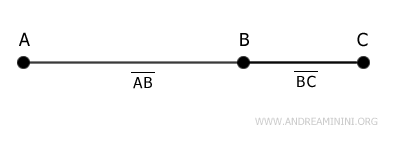
Dos segmentos son adyacentes si, además de ser consecutivos, pertenecen a la misma recta.
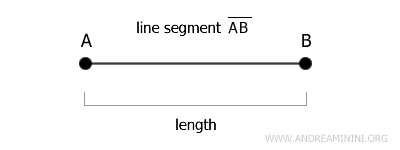
Todo segmento posee una longitud definida, que corresponde a la distancia entre sus extremos, y puede medirse en unidades como centímetros, metros u otras unidades de longitud.
Nota. Los segmentos se emplean en geometría para construir figuras más complejas. Además, desempeñan un papel esencial en el cálculo vectorial, pues representan la magnitud del vector que une dos puntos.
Los segmentos que tienen la misma longitud se denominan segmentos congruentes y, con independencia de su posición en el espacio, pertenecen a la misma clase.

Nota. En geometría, el concepto de congruencia se aplica a figuras que tienen la misma forma y tamaño, aunque se encuentren en posiciones diferentes. En el caso de los segmentos, dos segmentos son congruentes si tienen la misma longitud.
Por tanto, la longitud define una clase de equivalencia que agrupa a todos los segmentos congruentes.
Esto se diferencia de la medida de la longitud, que es simplemente un valor numérico. Por ejemplo: un segmento puede tener una longitud de 3 cm.
Y así sucesivamente.