Suma de Segmentos

Dados dos segmentos cualesquiera AB y CD, la suma de sus longitudes determina un nuevo segmento AD, cuya longitud es igual a la suma de las longitudes de AB y CD. $$ AB+CD = EF $$

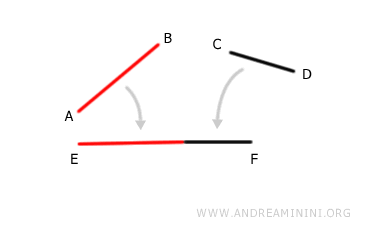
La suma de dos segmentos presenta las siguientes propiedades:

• Propiedad Conmutativa
  Para cualesquiera dos segmentos AB y CD, las sumas AB+CD y CD+AB son congruentes, es decir, poseen la misma longitud. $$ AB+CD \cong CD+AB $$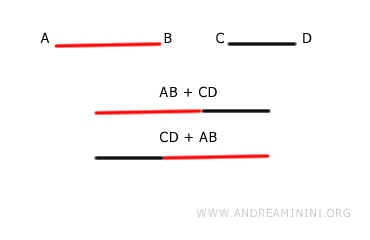

  

• Propiedad Asociativa
  Para cualesquiera tres segmentos AB, CD y EF, las sumas (AB+CD)+EF y AB+(CD+EF) son congruentes, lo que significa que miden exactamente lo mismo. $$ (AB+CD)+EF \cong AB+(CD+EF) $$
• Elemento Neutro
  El segmento nulo actúa como elemento neutro en la suma de segmentos. Al sumar cualquier segmento AB con el segmento nulo AA, se obtiene nuevamente el mismo segmento AB. $$ AB + AA = AA+AB = AB $$
• Suma de Segmentos Congruentes
  Si los segmentos AB y CD son congruentes $$ AB \cong CD $$ y los segmentos EF y GH también lo son $$ EF \cong GH $$, entonces sus sumas resultan congruentes. $$ AB+EF \cong CD+GH $$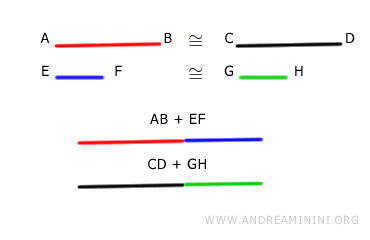

  

• Suma de Segmentos No Congruentes
  Si consideramos dos segmentos no congruentes $$ AB > CD $$ y otros dos segmentos no congruentes $$ EF > GH $$, las sumas de estos segmentos también resultarán no congruentes, manteniendo el mismo orden de desigualdad. $$ AB+EF > CD + GH $$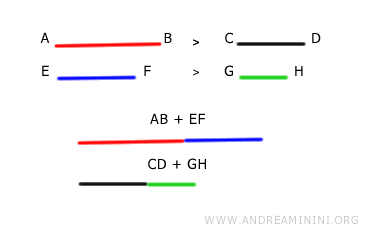

  

Y así sucesivamente.