Punto Medio de un Segmento de Recta
El punto medio de un segmento de recta AB es aquel que se encuentra exactamente a la misma distancia de los extremos A y B.

En cualquier segmento de longitud distinta de cero, existe un único punto medio que lo divide en dos partes idénticas.
Por ejemplo, consideremos el segmento de recta AB.

Este segmento contiene infinitos puntos, pero solo uno lo divide en dos segmentos congruentes, es decir, en dos segmentos de igual longitud.
En este caso, el punto medio es el punto C.
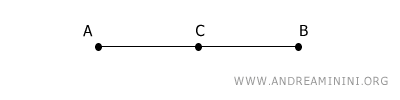
El punto C divide el segmento AB en dos partes, AC y CB, que son congruentes entre sí.
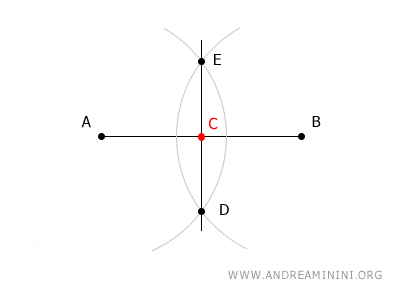
¿Cómo se determina el punto medio de un segmento? Para hallar el punto medio de un segmento, se puede usar un compás para trazar dos arcos con centro en los extremos del segmento. Es fundamental que el radio sea mayor a la mitad de la longitud del segmento. Las intersecciones de estos arcos definen dos puntos, D y E, sobre la recta que corta al segmento AB en su punto medio C.
Si se tienen dos puntos en el plano, $ A(x_A;y_A) $ y $ B(x_B;y_B) $, que son los extremos de un segmento AB, el punto medio M tendrá las siguientes coordenadas:
$$ x_M = \frac{x_A+x_B}{2} $$
$$ y_M = \frac{y_A+y_B}{2} $$
Las coordenadas de M se obtienen promediando las coordenadas x e y de los extremos.
Cálculo del Punto Medio en Geometría Analítica
Las coordenadas M(xM;yM) del punto medio M de un segmento en el plano cartesiano se determinan calculando el promedio de las coordenadas x e y de los puntos A(xA;yA) y B(xB;yB).

La coordenada x del punto medio es la media aritmética de las coordenadas x de los extremos del segmento, xA y xB.
$$ x_M = \frac{x_A+x_B}{2} $$
La coordenada y del punto medio es la media aritmética de las coordenadas y de los extremos, yA y yB.
$$ y_M = \frac{y_A+y_B}{2} $$
Por lo tanto, el punto medio del segmento AB se localiza en las coordenadas $ (x_M, y_M) $.
¿Y en el espacio tridimensional?
Si el segmento AB se encuentra en el espacio tridimensional, se sigue el mismo criterio: basta con promediar las coordenadas x, y y z de los extremos A y B.
$$ x_M = \frac{x_A + x_B}{2} $$
$$ y_M = \frac{y_A + y_B}{2} $$
$$ z_M = \frac{z_A + z_B}{2} $$
En este caso, el punto medio se define por las coordenadas $ (x_M, y_M, z_M) $.
Un Ejemplo Práctico
Supongamos que tenemos un segmento AB con extremos en A(2;3) y B(6;5).
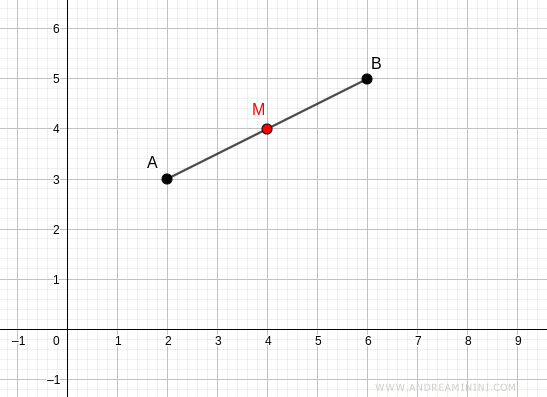
Las coordenadas del punto medio se calculan así:
$$ x_M = \frac{2+6}{2} = 4 $$
$$ y_M = \frac{3+5}{2} = 4 $$
Por lo tanto, el punto medio M del segmento AB está en (4;4).
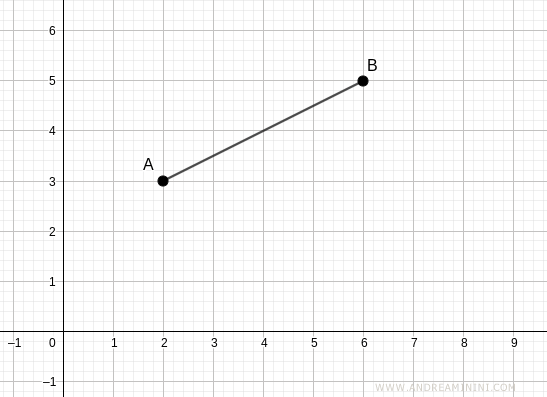
Ejemplo 2
Veamos otro segmento AB, cuyos extremos están en A(2;1) y B(6;3).
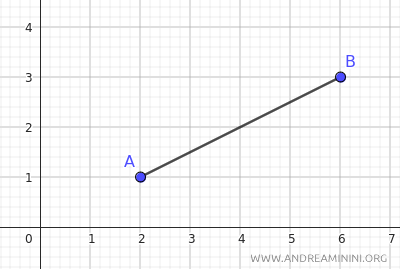
El punto A se encuentra en (2;1), por lo que xA=2 e yA=1. El punto B está en (6;3), con xB=6 e yB=3.
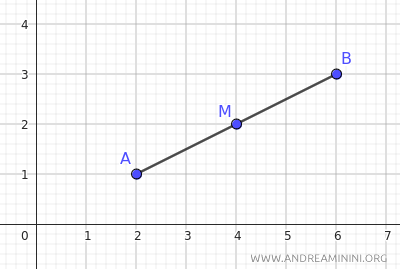
Calculemos las coordenadas del punto medio M:
$$ x_M = \frac{x_A+x_B}{2} = \frac{2+6}{2} = \frac{8}{2} = 4 $$
$$ y_M = \frac{y_A+y_B}{2} = \frac{1+3}{2} = \frac{4}{2} = 2 $$
Así, el punto medio del segmento se encuentra en (xM;yM) = (4;2).
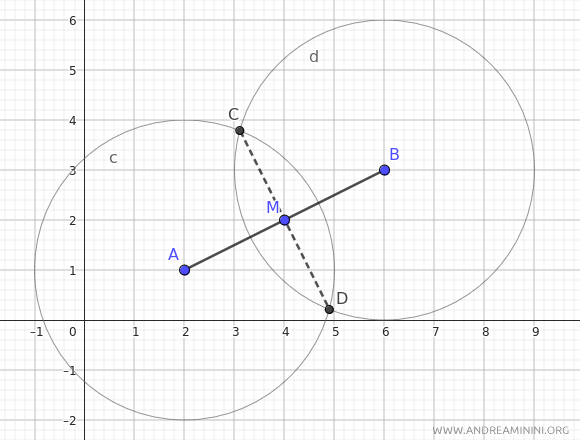
Para verificarlo, se pueden trazar dos arcos o circunferencias con el mismo radio, siempre mayor que la longitud de AM, centrados en A y en B. Luego, se unen con una recta los puntos de intersección C y D de los arcos. La recta CD cortará el segmento AB exactamente en su punto medio M.
La Demostración
Consideremos el segmento AB y su punto medio M.
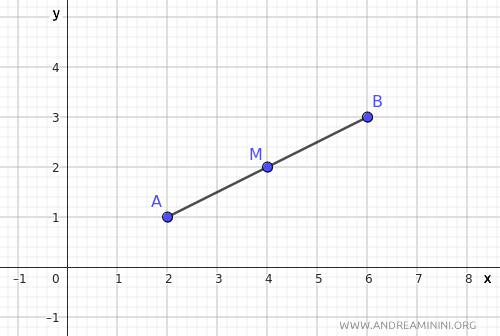
Ahora tracemos rectas paralelas al eje y que pasen por los puntos A, M y B.
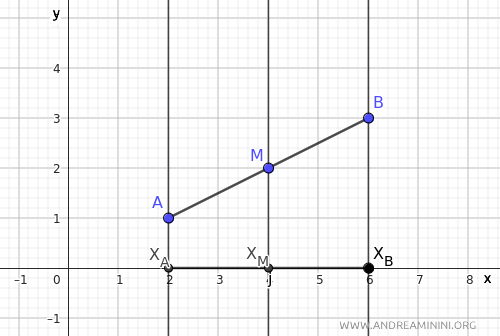
Estas tres rectas paralelas son cortadas por dos transversales: AB y xAxB.
Según el teorema de haces de rectas paralelas, los segmentos congruentes sobre una transversal corresponden a segmentos congruentes sobre la otra.
Como M es el punto medio de AB, los segmentos AM y MB son congruentes. Esto implica que los segmentos xAxM y xMxB también lo son.
En otras palabras, si M divide el segmento AB en dos partes iguales, también divide en partes iguales el segmento XAXB.
$$ | x_M - x_A | = | x_B - x_M | $$
Dado que xA<xM<xB, se puede eliminar el valor absoluto.
$$ x_M - x_A = x_B - x_M $$
Resolviendo para xM obtenemos:
$$ x_M + x_M = x_B + x_A $$
$$ 2x_M = x_B + x_A $$
$$ x_M = \frac{ x_B + x_A }{2} $$
Esto nos da la coordenada x del punto medio del segmento AB.
Después, aplicamos el mismo procedimiento para calcular la coordenada y del punto medio M.
Se trazan tres rectas paralelas al eje x que pasan por los puntos A, B y M.
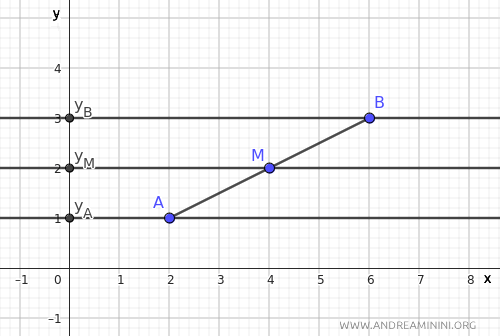
Estas rectas paralelas también son cortadas por dos transversales: AB y yAyB.
De acuerdo con el teorema de haces de rectas paralelas, si los segmentos AM y MB son congruentes, los segmentos correspondientes yAyM y yMyB también lo serán.
En otras palabras, si M divide el segmento AB en dos partes iguales, también divide en dos partes iguales su proyección yAyB sobre el eje y.
$$ | y_M - y_A | = | y_B - y_M | $$
Dado que yA<yM<yB, podemos eliminar el valor absoluto.
$$ y_M - y_A = y_B - y_M $$
Resolviendo para yM se obtiene:
$$ y_M + y_M = y_B + y_A $$
$$ 2y_M = y_B + y_A $$
$$ y_M = \frac{ y_B + y_A }{2} $$
Esto nos da la coordenada y del punto medio de AB.
En resumen, las coordenadas del punto medio M del segmento AB son:
$$ x_M = \frac{ x_B + x_A }{2} $$
$$ y_M = \frac{ y_B + y_A }{2} $$
Y así sucesivamente.