Teorema del Haz de Rectas Paralelas
Si un haz de rectas paralelas es cortado por dos rectas transversales, a segmentos congruentes sobre una transversal les corresponden segmentos congruentes sobre la otra transversal.
Un Ejemplo Práctico
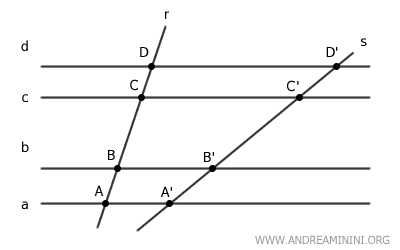
Por ejemplo, consideremos un haz de rectas paralelas (a, b, c, d) y dos rectas transversales r y s.
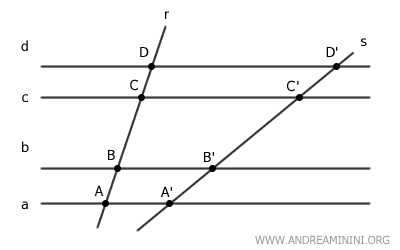
Nota. Un haz de rectas paralelas es un conjunto de rectas que son todas paralelas entre sí. Por ejemplo, las rectas a, b, c y d son paralelas entre sí.
Las rectas paralelas intersectan a la transversal r en los puntos A, B, C y D, y a la transversal s en los puntos A', B', C' y D'.
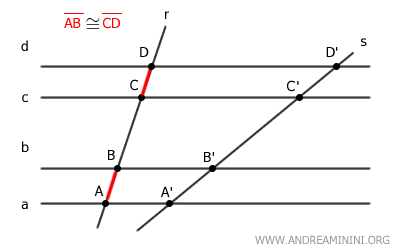
Supongamos que los segmentos AB y CD sobre la transversal r son congruentes, es decir, tienen la misma longitud: AB≅CD.
$$ \overline{AB} \cong \overline{CD} $$
Según el teorema del haz de rectas paralelas, a estos segmentos congruentes AB≅CD les corresponden segmentos congruentes A'B'≅C'D' sobre la otra transversal s.
$$ \overline{A'B'} \cong \overline{C'D'} $$
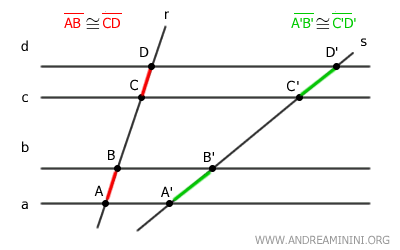
Los extremos de los segmentos correspondientes A'B' y C'D' sobre la otra transversal están determinados por las rectas paralelas que pasan por los mismos extremos de los segmentos AB y CD sobre la primera transversal.
Por ejemplo, la recta “a” pasa tanto por el punto A como por el punto A', que son los extremos inferiores de los segmentos AB y A'B'.
La Demostración
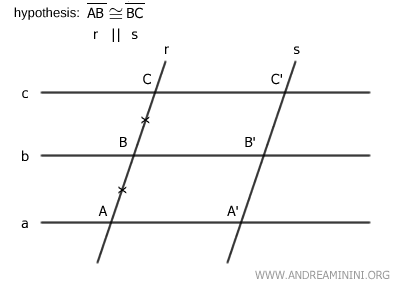
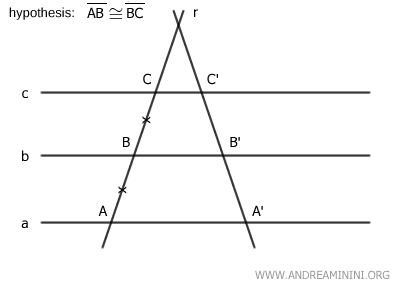
Para empezar, consideremos un haz de rectas paralelas (a, b, c) y dos rectas transversales r y s, con dos segmentos congruentes correspondientes AB≅BC sobre la transversal r.
$$ \overline{AB} \cong \overline{BC} $$
Queremos demostrar que existen dos segmentos correspondientes congruentes A'B'≅B'C' sobre la transversal s (tesis).
Para demostrar el teorema, se distinguen dos casos: cuando las transversales son paralelas y cuando se cortan.
A] Las Transversales Son Paralelas
En este caso, por hipótesis inicial, las rectas r y s son paralelas entre sí, es decir, r||s.
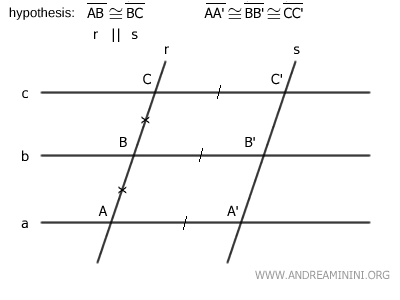
Como las transversales son paralelas, se deduce que los segmentos AA', BB' y CC' son congruentes, es decir, AA'≅BB'≅CC'.
La figura AA'B'B es un paralelogramo, pues ambos pares de lados opuestos son paralelos, por definición del haz de rectas paralelas a||b||c y por la hipótesis inicial r||s.
De forma análoga, la figura BB'C'C también es un paralelogramo por los mismos motivos.
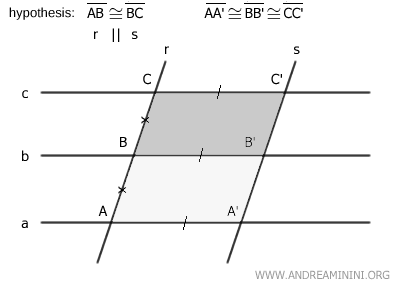
Sabiendo que los lados oblicuos de ambos paralelogramos AB≅BC son congruentes por hipótesis inicial, y que sus bases también lo son AA'≅BB', se concluye que los dos paralelogramos son congruentes AA'B'B≅BB'C'C.
$$ AA'B'B \cong BB'C'C $$
Por tanto, los dos paralelogramos poseen lados y ángulos congruentes en el mismo orden.
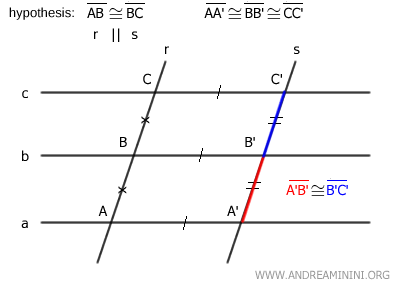
En particular, es importante destacar que los lados oblicuos AB≅A'B' y BC≅B'C' son congruentes.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Y dado que por hipótesis inicial AB≅BC, se concluye, por la propiedad transitiva, que los lados A'B'≅B'C' también son congruentes.
$$ \overline{A'B'} \cong \overline{B'C'} $$
En resumen, queda demostrado que los segmentos correspondientes A'B' y B'C' sobre la transversal s son congruentes si las dos transversales son paralelas.
B] Las Transversales No Son Paralelas
En este caso, por hipótesis inicial, las rectas r y s se cortan (no son paralelas).
Se traza la recta s', paralela a la recta s, de manera que corte a la recta r en el punto C.
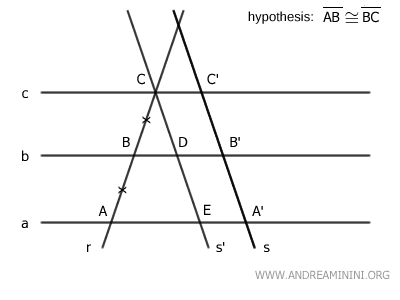
Luego se traza una segunda recta s'' paralela a s y que pasa por el punto B.
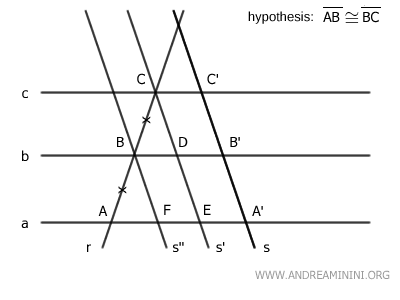
La figura CDB'C' es un paralelogramo y, por definición, posee lados opuestos congruentes.
Así se deduce que CD≅B'C'.
$$ \overline{CD} \cong \overline{B'C'} $$
La figura BFA'B' también es un paralelogramo y tiene lados opuestos congruentes.
Por lo tanto, se deduce que BF≅A'B'.
Analicemos ahora los dos triángulos ABF y BCD.
Estos triángulos tienen un lado congruente AB≅BC por hipótesis inicial.
Además, presentan ángulos correspondientes congruentes α≅α' por el teorema de las rectas paralelas, ya que las rectas paralelas “a” y “b” son cortadas por la transversal s''.
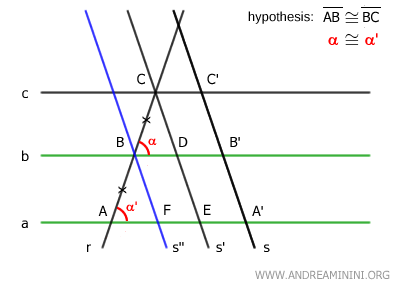
De igual manera, los ángulos correspondientes β≅β' son congruentes según el teorema de las rectas paralelas, ya que las rectas s' y s'' (paralelas) son cortadas por la transversal r.
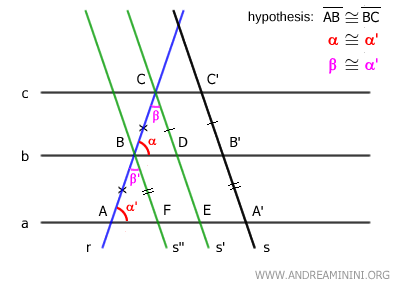
Los triángulos ABD≅BCD son congruentes según el segundo criterio de congruencia (Lado-Ángulo-Lado) porque poseen un lado congruente AB≅BC y dos ángulos congruentes α≅α' y β≅β'.
Por tanto, ambos triángulos tienen sus lados y ángulos congruentes.
En particular, es relevante saber que los lados BF≅CD son congruentes.
$$ \overline{BF} \cong \overline{CD} $$
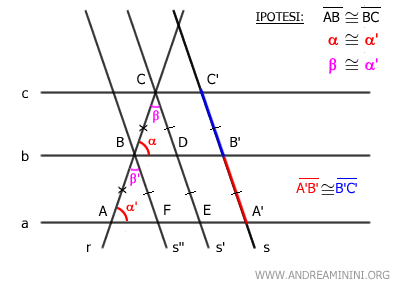
Como se sabe que CD≅B'C' y BF≅A'B', por la propiedad transitiva se concluye que A'B'≅B'C'.
$$ \overline{A'B'} \cong \overline{B'C'} $$
En conclusión, ha quedado demostrado que los segmentos correspondientes A'B' y B'C' sobre la transversal s son congruentes si las dos transversales se cortan.
Y así sucesivamente.