Postulado de las paralelas
El postulado de las paralelas, también conocido como el quinto postulado de Euclides, afirma lo siguiente:
Dada una recta r y un punto P exterior a ella, existe una única recta paralela a r que pasa por el punto P.
Se trata de un postulado porque la unicidad de la paralela no se deduce de otros teoremas o propiedades de las rectas, sino que se acepta como un principio fundamental.
Sin embargo, la existencia de una paralela a r que pase por P puede demostrarse mediante el teorema de las rectas paralelas, identificando un par de ángulos alternos internos congruentes α≅β.
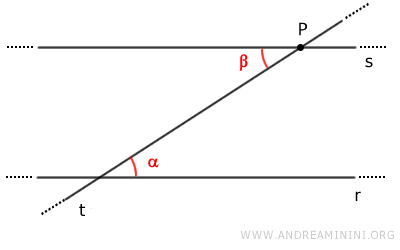
Nota: Este postulado es conocido como quinto postulado de Euclides, aunque su formulación actual se atribuye a Proclo, matemático y filósofo bizantino del siglo V d. C.
La demostración
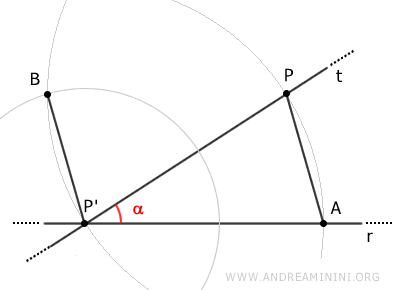
Consideremos una recta r y un punto P en el plano, exterior a dicha recta.
Seleccionamos un punto P' sobre la recta r.
Después, trazamos una recta t que pase por los puntos P' y P.
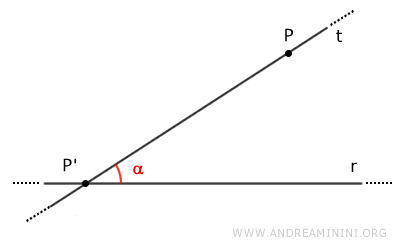
La recta t forma un ángulo interno alfa (α) con la recta r.
Con centro en P' y radio PP', trazamos un arco que corta a la recta r en el punto A.
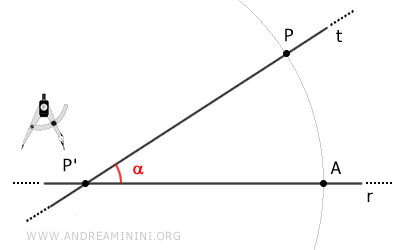
Sin cambiar el radio, colocamos el compás en P y trazamos un segundo arco que pase por P'.
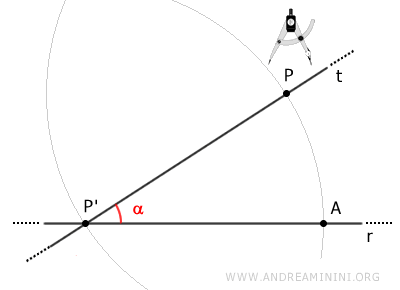
Unimos los puntos A y P mediante el segmento AP.
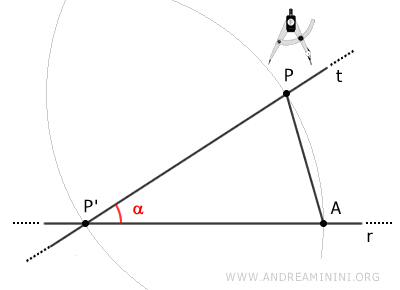
Con centro en P' y radio AP, trazamos un tercer arco que interseca al segundo en el punto B.
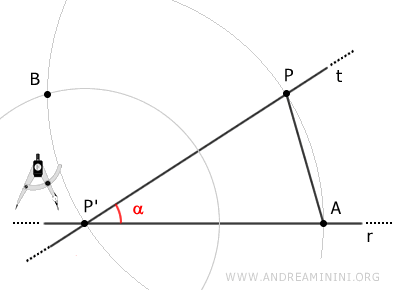
Unimos los puntos P' y B con el segmento BP'.
Finalmente, trazamos una recta s que pase por los puntos B y P.
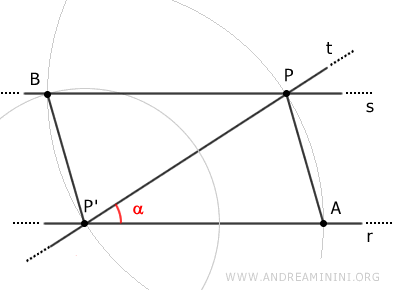
Entre las rectas r y s se forman los triángulos APP' y BPP'.
Según el tercer criterio de congruencia de triángulos, dichos triángulos son congruentes, ya que presentan lados correspondientes de igual longitud.
$$ APP' \cong BPP' $$
Como son congruentes, sus ángulos correspondientes también lo son.
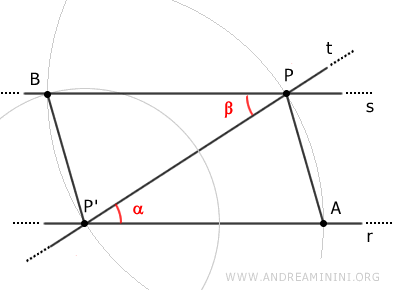
Por lo tanto, el ángulo alfa es congruente con el ángulo beta.
$$ \alpha \cong \beta $$
Los ángulos alfa y beta son ángulos alternos internos congruentes (α≅β).
En consecuencia, y de acuerdo con el teorema de las rectas paralelas, las rectas r y s son paralelas.
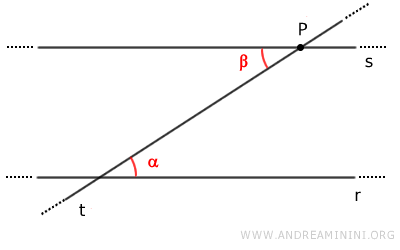
Hemos demostrado así la existencia de una recta s paralela a la recta r que pasa por el punto P.
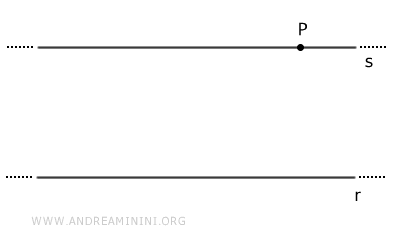
Nota: Como se ha indicado, la unicidad de la recta paralela s no puede demostrarse a partir de otras propiedades. Por ello se acepta como un postulado.
¿Por qué no se puede demostrar la unicidad?
El propio Euclides reconoció que su llamado quinto postulado resultaba menos evidente y “natural” que el resto de sus axiomas. Por ello procuraba emplearlo lo menos posible y solo cuando era estrictamente necesario.
Durante siglos, numerosos matemáticos intentaron deducir el quinto postulado a partir de los cuatro primeros, sin éxito. Es un postulado independiente. Todos los intentos de demostración terminaban basándose - con frecuencia de manera inconsciente - en hipótesis equivalentes al propio postulado.
En su afán por probar que solo puede pasar una paralela por un punto exterior a una recta (la unicidad), como sostenía Euclides y sugería la intuición, algunos llegaron incluso a modificar el propio postulado.
En lugar de encontrar una contradicción, lo que descubrieron fue un marco geométrico alternativo, plenamente coherente en sí mismo.
Nota: Girolamo Saccheri intentó una demostración por reducción al absurdo: elaboró una geometría hipotética sin el quinto postulado, esperando encontrar alguna incoherencia. Sin embargo, no encontró contradicción alguna.
Estos esfuerzos dieron origen, en el siglo XIX, al desarrollo de las geometrías no euclidianas, en las que el quinto postulado se sustituye por un supuesto distinto:
- Geometría hiperbólica (Lobachevsky, Bolyai): En este contexto, por un punto exterior a una recta dada pueden pasar infinitas paralelas, y la suma de los ángulos internos de cualquier triángulo es inferior a 180°.
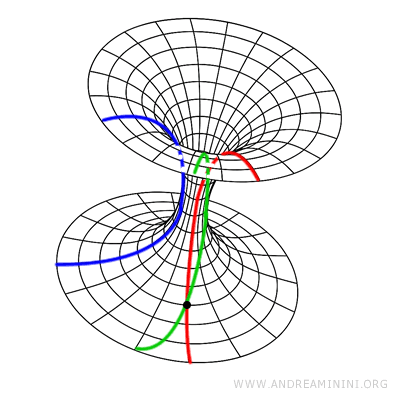
Nota: Los trabajos pioneros de Saccheri, Lobachevsky y Bolyai no bastaron por sí solos para garantizar la coherencia lógica de la geometría hiperbólica. Este logro se alcanzó más tarde gracias a Felix Klein y Henri Poincaré, quienes construyeron modelos de geometría hiperbólica dentro de la geometría euclidiana. Así demostraron que, si la geometría euclidiana es coherente, también lo es la hiperbólica. En el modelo de Klein, por ejemplo, el "plano" se representa como el interior de un círculo, y las "rectas" como cuerdas de dicho círculo.
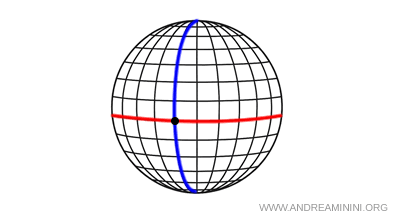
- Geometría elíptica (Riemann): En este caso, no existe ninguna paralela que pase por un punto exterior a una recta. Además, la suma de los ángulos internos de un triángulo supera los 180°. En una esfera, por ejemplo, no existen paralelas, ya que todas las "rectas" son círculos máximos que inevitablemente se cortan.
El descubrimiento de las geometrías no euclidianas constituye uno de los grandes hitos matemáticos del siglo XIX.
Demostró que muchas propiedades que antaño se consideraban “universales” dependen, en realidad, del quinto postulado, y que los axiomas de Euclides no son el único cimiento sobre el que construir una geometría coherente.
También ayudó a redefinir el propio concepto de axioma: ya no como una verdad absoluta, sino como un supuesto que determina el marco lógico de un sistema matemático.
Más allá de lo estrictamente matemático, el surgimiento de las geometrías no euclidianas mostró que la propia noción de espacio no es absoluta, y que puede concebirse de formas diversas y perfectamente válidas. Un descubrimiento con profundas repercusiones tanto en matemáticas como en física.
En definitiva, el quinto postulado nos enseña que no existe una única "geometría verdadera", sino múltiples geometrías posibles, siendo la euclidiana solo un caso particular. Ahora bien, sigue abierto el interrogante sobre cuál de ellas describe mejor la realidad física. Según la teoría de la relatividad de Einstein, la gravedad curva el espacio. Cerca de los agujeros negros, por ejemplo, esta curvatura se vuelve extrema. Por tanto, para comprender la geometría global del universo, es preciso determinar si es plano (euclidiano) o curvo (no euclidiano). La evidencia actual sugiere que, de existir alguna curvatura, esta sería mínima, de modo que el universo parece casi plano.
Y la historia sigue su curso.